Integers Definition Math

The Integer is a Latin word which means whole. Integers are considered unique sets because they contain negative numbers, positive numbers and zero, and it does not include fractions and decimals.

Common examples of the Integers are -1, -2, -3, -4, -5, 5, 3,2, 1 ...

Types of Integers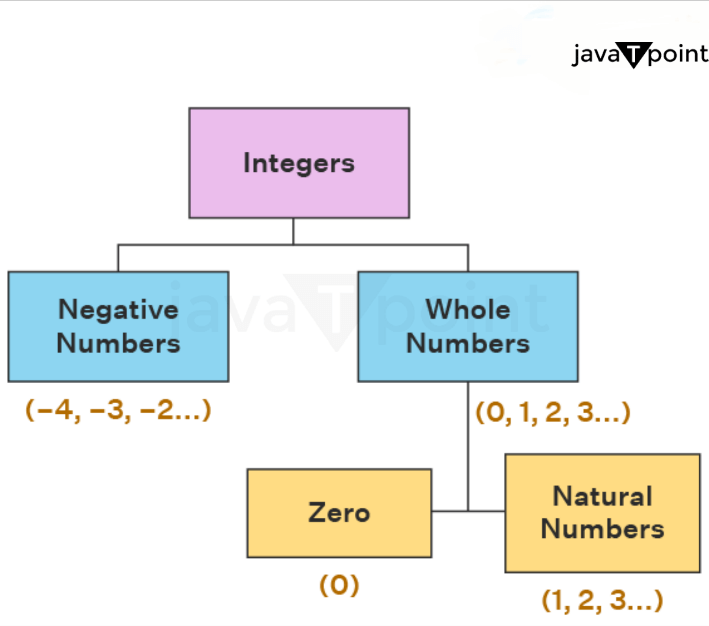

There are three types of integers: Negative, Positive, and Zero. Comprehensive classification of the Integers includes Natural numbers, Even integers, Odd integers, Prime integers, Whole number integers, composite integers, etc.

Representing Integers on the Number Line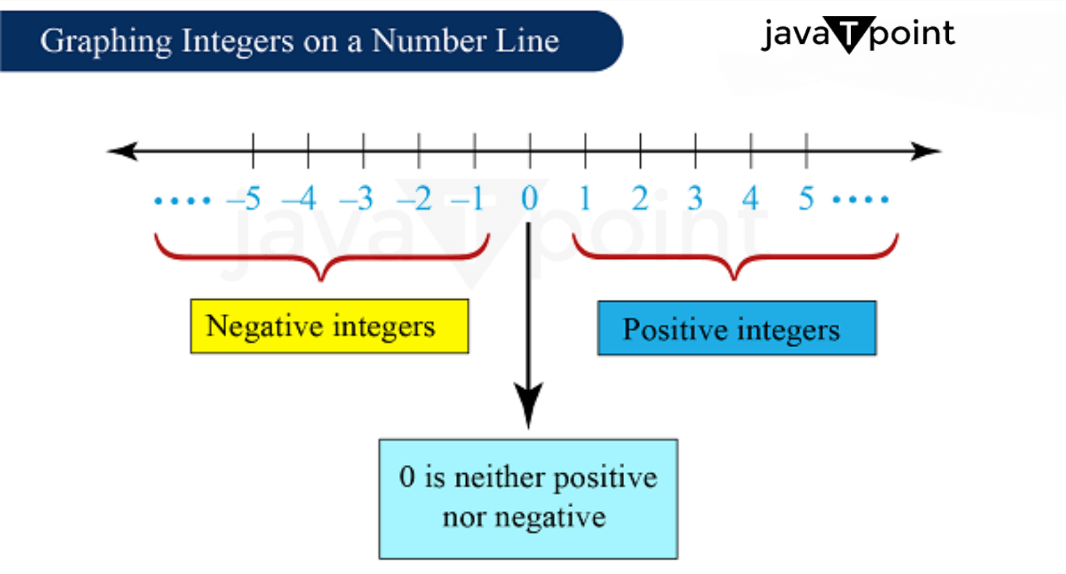

The number line is a graphical representation of the number. Positive numbers are represented on the right side of the number line, and negative numbers are represented on the left side of the number line. The zero remains at the centre of the number.

History of the Integers

The concept of integers came into existence in the year 1563. Arbermouth Holst was engrossed in his bunnies experiment. He continuously counts bunnies in the cage after six months, and he gets to know that the bunnies have increased. From that, an idea came to his mind to develop a number system of adding and Multiplication. He almost gave 15 years to produce a concept of the number system.

Later the work was continued by the Japanese Mathematician in the 1890s, who developed the concept called integers. The Latin meaning is "untouched." Indians, Babylonians, and Mayans invented the Zero independently. Some researchers point out that the finding of the Babylonians influenced the Indian Number system.

Indian Mathematician had supported the concept of Zero, and before that official creation of zero was not endorsed by any countries until it spread to the Indian subcontinent. The negative number received acceptance in the 19^th century in the number system.

• Indian Contribution

Brahmagupta, an Indian Mathematician, was acclaimed for using negative numbers around 630 AD. At this time, positive numbers were applied to denote assets and negative numbers to denote liability (debt).

• Chinese Contribution

Chinese are acclaimed for using negative numbers, and they were the first culture to recognize and use negative numbers. Negative numbers were represented using red rods.

• European Contributions

Europeans started using negative numbers in 1545, and the Italian Mathematician Girolamo Cardano presented that negative numbers would be very useful.

The further advancement in algebra in the Arab world developed the understanding of the integers. The French Mathematician Fermat laid the foundation of the modern number theory.

Contemporaries' concept of integers is the advanced stage of integers, and they are used in diverse fields such as finance, physics, computer programming, engineering, and physics. The study and continuous research in the integers remain active.

Rules for Adding Integers

Rules for the Subtraction of the Integers

Rules for the Multiplication of the Integers

Rules for the Division of the Integers

Properties of the Integers

1. Identity Property for Addition

The addition of the zero to any integer value does not alter the value of the integer number.

For example

9 + 0 = 9

2. The Identity Property for Multiplication

Multiplication of 1 to any integer value does not produce any alteration in the value of the number.

For example,

-9 x 1 = -9

3. Inverse Property of the addition

The sum of the integer value and its additive inverse produce zero.

For example

-5 + 5 = 0

4. Zero Property Multiplication of Integer

Any number which is multiplied by zero produces the result zero.

For example

-10000 x 0 = 0

Question: Evaluate the following

1. 22 - ( -45)
2. 45 + (-10)
3. - 56 + -40
4. -34 - (-60)

Solution

1. 22 - (-45) = 22 + 45 = 67
2. 45 + (-10) = 45 -10 = 35
3. -56 + - 40 = -96
4. -34 - (-60) = -34 + 60 = 26