Young's Modulus Definition

Today, let's study Young's modulus covering the definition, unit, dimensions, and applications. We'll be learning about the elastic moduli of steel, glass, wood, and plastic. Let's study the modulus of elasticity in the following section and take a look at a few examples.

The object's stress-strain connection is measured by the object's modulus of elasticity. The most important factor in determining how much concrete will bend when exposed to stress is its modulus of elasticity. Elastic constants are the physical constants that control the degree to which a material can deform in response to a certain stress system.

What is Young's Modulus?

Young's modulus constitutes a numerical constant which explains the elastic nature of something solid experiencing compression or tension in only a single direction, like in the situation of an iron rod that, soon after being bent or compressed along the length, comes back to its initial length. It was given its name after the 18th-century English physician and physicist Thomas Young.

Young's modulus is a measurement of how well a substance is able to endure fluctuations in length when placed under compression or tension within its length. Calculating Young's modulus necessitates dividing the stress along the longitudinal axis by the longitudinal strain, also known as the modulus of elasticity or simply the Young's modulus. Strain and stress may be described in terms of a metal bar that is experiencing tension as follows.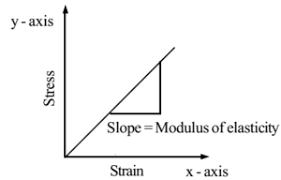

A metal bar that has a cross-sectional size of A grows from its original length L0 into a new length Ln whenever a force F is thrust to the two sides of the bar. Corresponding to this, the cross-section decreases. The ratio, or F/A, that establishes the stress is the tensile strength divided by the cross-sectional area. The length change, determined as Ln L0, divided by the initial length, calculated as (Ln L0)/L0, is the strain or relative deformation. A strain has no dimensions. Thus, Young's modulus can be mathematically represented as:

Young's modulus = stress/strain = (FL0)/A (Ln − L0).

This is a particular instance of Hooke's law of elasticity. The English system of measures uses pounds per square inch (psi) to determine Young's modulus, whereas the metric system uses newtons per square metre (N/m2). Approximately roughly 1.0 107 psi or 7.0 1010 N/m2, aluminium has a Young's modulus. The total number of bends for steel is approximately three times higher, implying that three times the amount of force is needed to bend an aluminum bar with a comparable form as a steel bar.

The range wherein the stress is in relation to the strain and the component recuperates to its original size following the elimination of the external force is the only circumstance in which Young's modulus has any relevance. When the substance experiences more strain, it can either flow, permanently bend, or eventually break.

A metal bar under stress will gradually lose some of its breadths as it expands. This lateral expansion results in transverse strain, which can be calculated by dividing the new breadth by the original breadth. Poisson's ratio refers to the relationship between transverse strain and longitudinal strain. Poisson's ratios for steel and aluminium alloys, respectively, have an average value of 0.28 and 0.33. When tested under longitudinal compression, the volume of a substance declines, and when taken to longitudinal tension, it rises if its Poisson ratio is less than 0.50.

History of Young's Modulus

In 1727, Swiss engineer and scientist Leonhard Euler explained the basic principle behind Young's modulus. Modern predictions of the modulus were made possible by evaluations carried out in 1782 by Italian scientist Giordano Riccati. However, British scientist Thomas Young, whose work mentioned the formula for the calculation of the modulus during his Course of Lectures on Natural Philosophy and the Mechanical Arts in 1807, has been linked with giving it its name. Considering the present knowledge of its historical context, it should probably be known as Riccati's modulus, but carrying out so would lead to uncertainty.

Materials with Anisotropy and Isotropy

The angle of incidence of a material often affects Young's modulus. Materials that demonstrate isotropy have consistent mechanical characteristics throughout. Ceramics and pure metals are a few examples. A material may develop grain structures that give it directional mechanical characteristics by processing it or introducing impurities to it. Based upon whether the force is applied perpendicular to the grain or directly on it, these materials that are anisotropic might've considerably differed from Young's modulus values. Carbon fibre, wood, & concrete that is reinforced are all excellent examples of anisotropic materials.

Usage of Young's Modulus

Young's modulus makes it possible to estimate how a bar constructed of an isotropic elastic material might differ in size when subjected to tensile or compressive forces. For example, it anticipates how much a substance sample will stretch or contract when compressed. When tensile or compressive stress exists in a particular direction, and no tension exists in the other directions, this is referred to as uniaxial stress, and Young's modulus immediately applies. For the purpose of forecasting the deflection that will take place in a statically determined beam when a force is put on it at a location in the space between the beam's supports, Young's modulus is used as well.

The bulk modulus K, Poisson's ratio v, and shear modulus G is a few more elastic properties often used in other elastic calculations. A material's elasticity in an isotropic state might be precisely determined by any two of these variables. For homogeneous isotropic materials, there are relatively straightforward relationships between the elastic constants that make it possible to calculate them all as long as two are known:

E= 2G(1+v) = 3K (1-2v)

1. Non-linear vs. Linear

Hooke's law, linking stress and strain, is represented by Young's modulus as the proportionality parameter. But Hooke's law can be considered valid when a linear and elastic response is anticipated. However, all solid materials demonstrate practically Hookean characteristics for small enough strains or stresses, suggesting that any genuine material would ultimately fail and shatter when stretched over a very wide distance or with a very strong force.

A material has been determined to be linear if the range of values across which Hooke's rule holds true is sufficiently wide relative to the usual stress that one would anticipate applying to the substance. Otherwise, the material is referred to be non-linear (if the normal stress one would apply is beyond the linear range).

In general, linear materials include materials like steel, carbon fiber, and glass, whereas non-linear materials include things like rubber and soil. Non-linear materials will respond proportionately to even the smallest stresses or strains, yet when linear materials undergo exposure to exceptionally massive stresses or strains, the linear theory is unsuitable. Therefore, this classification is not universal.

For instance, it would be silly to apply the linear theory to explain the catastrophic breakdown of a steel bridge since the linear theory assumes reversibility. Steel is a linear material for most purposes, but not in this situation. The tangent modulus is the term used in the theory of solid mechanics to describe the slope of the curve representing stress and strain at any particular location. An analytical meaning could be the slope of the stress-strain curve arising from tensile testing on a piece of the material.

2. Directional Materials

Young's modulus is not necessarily the same in certain orientations of a material. The majority of metals and ceramics, alongside many other substances, are isotropic, meaning that their mechanical characteristics are the same regardless of the orientation. However, some impurities might be included in metals and ceramics, and metals can be physically processed to give their grain structures directionality.

As a result, these substances become anisotropic, and the force vector's direction will affect how these materials' Young's modulus behaves. Many composites demonstrate anisotropy. For instance, when a force is applied parallel to the fibers (along the grain), carbon fiber has a substantially greater Young's modulus (is much stiffer). Reinforced concrete and wood are other examples of these materials. This directional phenomenon might be used by engineers to their favor while building buildings.

3. Temperature-Related Effects

The Young's modulus of metals varies with temperature and can possibly be realised by altering the interatomic bonding of the atoms; as a result, its change is discovered to be reliant on the alteration in the work function of the metal. The Rahemi-Li model illustrates the way modifications to the electron work function can cause modifications in Young's modulus of metallic substances and anticipates these variations with measurable variables using the generalization of the Lennard-Jones potential to solids, whereas traditionally, this modification has been anticipated by means of combining without there being a clear root cause (for example, the Watchman's formula).

Defining the Stress-Strain Curve.

In order to understand a material's rigidity, strength, ductility, and failing limitations, a stress-strain curve is used to illustrate how a material responds to loads. For instance, a ball made of rubber would get back its original form after being struck, unlike a glass marble, which would shatter into fragments the moment it hit the ground.

Stress-strain curves are the only method that can fully explain the variance in material behaviour between a rubber ball and a glass marble. A solid body's substance features have an impact on how it changes in response to a load. This frequently ends in an additional typical question: Why not base the substance's characteristics definition on a force-displacement relationship? Why do we take the stress-strain connection instead?

This is due to the simple reason that both displacement and force represent the material's extrinsic traits. The quantity of material present determines the force necessary to distort the material to a given level. As a result, it can be hard to describe a material using a force-displacement relationship as doing so would not provide the material a consistent mechanical attribute.

On the contrary, strain and stress serve as the opposites of force and displacement in terms of inherent material properties. For instance, a steel bar with a 10 mm diameter has the same capacity to withstand tension as a bar with a 10 cm diameter. Whenever an outside force (F) applies to an equilibrium component made of a continuous deformable substance, the part will deform.

The substance then attempts to maintain equilibrium through the development of internal forces that are equivalent to but opposite from the external loads in an attempt to counteract this deformation. If the external force is applied uniformly around the body, then a component of the external force (F) will pass via any cross-sectional part of the body (A), and an internal force (F') will work against this external action. The term "Stress" refers to this internal force in any particular cross-section, and it may be defined as: σ=F/A

What essential information should you have regarding this topic?

The stress-strain charts may look quite different for several kinds of substances. Brittle materials tend to be particularly durable as they can withstand great pressure, don't extend much, and shatter rapidly. Although ductile materials contain a greater elastic zone where the relationship between stress and strain is linear, this linearity breaks down at the initial changeover (the elastic limit), and the substance can no longer revert to its earlier shape.

The second highest point, representing the maximum tensile strength, provides information on the highest stress that a material can bear before failing. Despite not being very robust, plastic materials may bear considerable pressure. In a stress-strain figure, the gradient of the line indicates Young's modulus.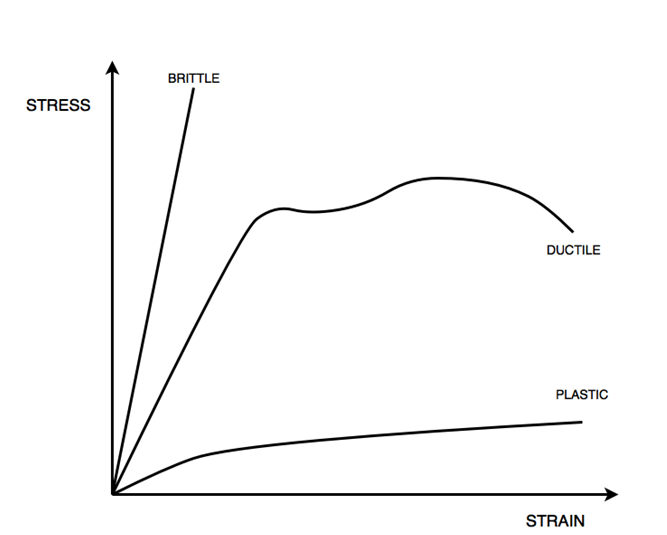

The stress-strain plot will consist of more points if multiple measurements have been taken using a range of masses, which will enhance the accuracy of Young's modulus calculation. Considering the wire's cross-sectional area to be considered is a further significant factor. It could prove beneficial to take the average of multiple micrometer measurements since the wire's imperfections might imply that the diameter is not exactly consistent along the whole length of the wire.

How can I use this for myself?

At the BUCS championships, Nick Cruchley won in the pole vault. It is of the utmost importance to learn how substances react mechanically because doing so enables us to create new goods and enhance those we already have by enabling us to better understand how materials behave. The development of vaulting poles, which high jump competitors rely on for improved performance, was one example of a study project at Birmingham.

These poles need to be lightweight to enable a quick run-up. However, they also need to be durable and prepared to store strain energy that is generated when the pole bends. The pole must be able to transform elastic energy into kinetic energy when it straightens out, sustain the strain imposed by the vaulter's weight, and endure numerous uses by the athlete. Many items manufactured on small scales consist of biological and non-biological microparticles, such as pharmaceutical medications, reproductive medications, and tissue engineering, as well as chemicals, home goods, and agricultural products.

Studying how they work allows us to anticipate how they will behave throughout production and processing, allowing us to optimise their performance potential. A material's Young's modulus is a crucial attribute to understand in order to forecast how the material will respond to a force. This is crucial for everything around us, including buildings, bridges, cars, and more.