Equilateral Triangle Definition

Introduction: Explaining the Concept of Equilateral Triangles

Geometry is a branch of mathematics that studies points, lines, angles, shapes, and their relationships. One of the fundamental concepts in geometry is the triangle, a polygon with three sides and three angles. The equilateral triangle is among the most important and interesting among the numerous types of triangles.

An equilateral triangle is a form of triangle where all three sides are of equal length. In other terms, an equilateral triangle is a regular polygon with three sides. The term "equilateral" derives from the Latin word "aequus," which means "equal," and "latus," which means "side."

Equilateral triangles have several unique properties that distinguish them from other triangles. For example, all three angles of an equilateral triangle are equal, and each angle measures 60 degrees. This property is not found in any other form of a triangle. Equilateral triangles are also symmetrical, meaning they can be divided into two congruent halves by a line passing through their centroid.

Equilateral triangles are essential in geometry for several reasons. They are the simplest and most symmetric form of a regular polygon, and many other geometric shapes can be derived from them. Equilateral triangles are also common in nature and human-made structures, such as bridges, turrets, and buildings.

Understanding the concept of equilateral triangles is essential in geometry as it forms the basis for further learning in this field. Equilateral triangles have essential applications in other areas, such as engineering, architecture, and design. The following sections will investigate the definition, properties, construction, examples, and real-life applications of equilateral triangles.

Definition of an Equilateral Triangle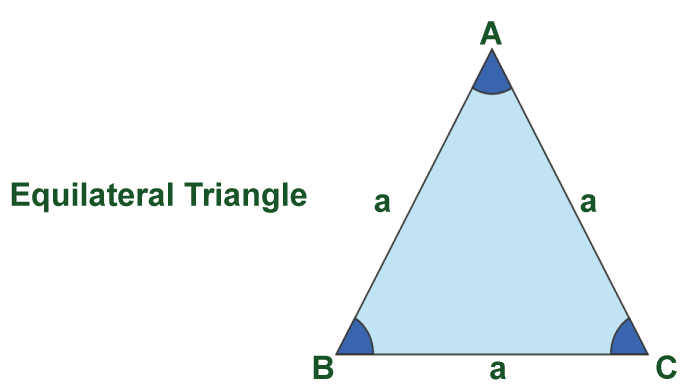

In mathematical terms, an equilateral triangle can be defined as a polygon with three sides of equal length and three angles of equal measure. Each angle of an equilateral triangle measures 60 degrees, also known as a "regular" polygon.

The sides of an equilateral triangle are also known as "congruent" sides because they have the same length. The opposite angles of an equilateral triangle are also congruent. If one angle of a triangle is measured as 60 degrees, it implies that all three arches of the triangle are equal to 60 degrees.

Another essential property of an equilateral triangle is its symmetry. An equilateral triangle is symmetrical about its center, also known as the centroid. By drawing a line that passes through the centroid of an equilateral triangle, we can divide the string into two congruent equal sections.

Equilateral triangles can also be classified as isosceles triangles, which are triangles with two sides of equal length, or as scalene triangles, which are triangles with no equal sides. However, equilateral triangles are unique because they are the only form of a triangle that is also regular.

In summation, an equilateral triangle is a polygon with three congruent sides and three congruent angles. The sides are of equal length, and each angle measures 60 degrees. Equilateral triangles are symmetrical about their center, making them an essential concept in geometry and other related fields.

Properties of an Equilateral Triangle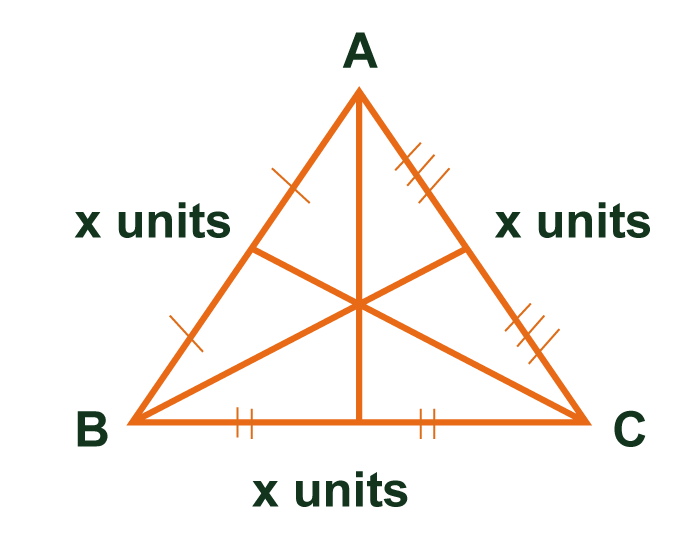

Equilateral triangles have several unique properties that distinguish them from other triangles. Here are some of the key properties of equilateral triangles:

• Equal Sides: An equilateral triangle has three sides of equal length. It can be inferred that the distance between any two points on the perimeter of an equilateral triangle is constant and equal.
• Equal Angles: All three angles of an equilateral triangle are congruent and measure 60 degrees. This property is unique to equilateral triangles and is not found in any other type of triangle.
• Symmetry: An equilateral triangle is symmetric about its center, also known as the centroid. Drawing a line through the centroid of an equilateral triangle allows the triangle to be divided into two identical parts that are congruent.
• Regular Polygon: An equilateral triangle is a regular polygon, meaning all its sides and angles are equal. It is the simplest and most symmetric type of regular polygon.
• Area Formula: The area of an equilateral triangle can be calculated using the formula A = (sqrt(3)/4) * a^2, where A is the area, and a is the length of the side.
• Height Formula: The height of an equilateral triangle can be calculated using the formula h = (sqrt(3)/2) * a, where h is the height and a is the length of the side.
• Inscribed Circle: An equilateral triangle has a unique inscribed circle, also known as the incircle, which touches all three sides of the triangle at its midpoint. The incircle's radius equals one-third of the triangle's height.
• Circumscribed Circle: An equilateral triangle also has a unique circumscribed circle, which passes through all three vertices of the triangle. The radius of the circumscribed circle is equal to the length of the side divided by the square root of three.

In summary, equilateral triangles have several unique properties that make them an essential concept in geometry. They have equal sides and angles, are symmetric, and have a special inscribed and circumscribed circle. The formulas for calculating the area and height of an equilateral triangle are also specific to this type of triangle.

Construction of an Equilateral Triangle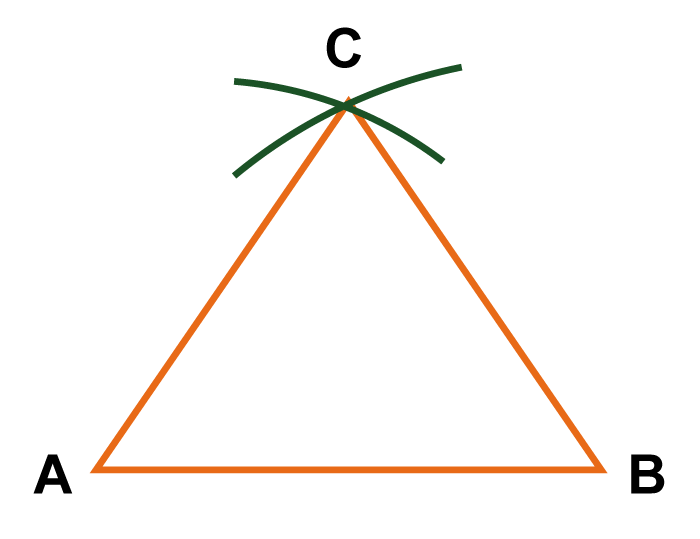

There are several methods to construct an equilateral triangle, but one of the simplest and most common methods is using a straightedge and compass. Here are the methods for creating an equilateral triangle:

• Draw a straight line segment of any length using a straightedge.
• Place the point of the compass at one end of the line segment and draw an arc across the line.
• Without changing the compass width, position the point of the compass at the other end of the line segment and draw another arc that intersects the first arc.
• Use the straightedge to draw a line connecting the two locations where the arcs intersect. This line segment will be on one side of the equilateral triangle.
• Place the point of the compass at one end of the line segment and draw an arc that intersects the line segment at a point. Label this location as A.
• Using the same compass width, position the point of the compass at the other end of the line segment and draw an arc that intersects the line segment at a point. Label this location as B.
• Without changing the compass width, position the point of the compass at point A and draw an arc that intersects the first arc at a point. Label this location as C.
• Draw a line linking points B and C, and then connect the points A and C. These two lines will conclude the equilateral triangle.

Alternatively, folding a piece of paper is another approach to constructing an equilateral triangle. Here are the instructions for this method:

• Take a rectangular piece of paper and fold it in half lengthwise.
• Unfold the paper and then fold it in half widthwise.
• Unfold the paper again, and you should see a crease down the middle in the shape of a cross.
• Fold the top left corner of the paper down to meet the center crease.
• Repeat the same fold with the top right corner of the paper.
• Fold the bottom edge of the paper up to meet the crease formed by the previous two folds.
• Unfold the paper; you should have an equilateral triangle formed by the creases.

In summary, there are different methods to construct an equilateral triangle, but the most common approach is using a straightedge and compass. This method involves sketching arcs and connecting points to form a triangle. Another technique is folding a piece of paper to construct an equilateral triangle using creases.

Examples and Real-Life Applications of Equilateral Triangles

Equilateral triangles are important in geometry and have real-life applications in different fields. Here are some examples and real-life applications of equilateral triangles:

• Construction: Equilateral triangles are commonly used in construction for creating stable structures. One example is the truss bridge, made of equilateral triangles to distribute the bridge's weight evenly.
• Electronics: Equilateral triangles create a balanced three-phase power system in electronic circuitry. The three-phase system provides a more stable and efficient power source for large-scale applications like power plants and factories.
• Astronomy: In astronomy, the three stars that form the Orion constellation are arranged in an equilateral triangle shape. Astronomers have used this triangle shape to measure the distance to other stars and galaxies.
• Art: Equilateral triangles are used in various art forms, including abstract art and logo design. For example, the Mercedes-Benz logo uses an equilateral triangle with a star inside, symbolizing the brand's aspirations for success in land, air, and sea transportation.
• Packaging: In packaging, equilateral triangles are used to create tetrahedron-shaped containers, which are used for packaging different products like tea bags and sugar packets.
• Pyramids: The Great Pyramids of Giza, one of the most famous ancient structures in the world, are built using equilateral triangles as the base of each pyramid.
• Navigation: Equilateral triangles are used in navigation for measuring distances between objects. By using triangulation, sailors and pilots can determine their position and navigate accurately.

In summary, equilateral triangles have several real-life applications in different fields. They are used in construction, electronics, astronomy, art, packaging, pyramids, and navigation. Equilateral triangles provide a stable and balanced structure that can distribute weight evenly, create efficient power systems, and help us navigate and measure distances accurately.

Conclusion: Importance of Understanding Equilateral Triangles in Geometry

In conclusion, comprehending equilateral triangles in geometry is essential for academic and real-life applications. Equilateral triangles are special triangle forms with unique properties and characteristics. These properties benefit them in several fields, including construction, electronics, astronomy, art, packaging, and navigation.

Studying equilateral triangles helps students develop critical thinking and problem-solving abilities. It also helps students comprehend the relationships between the different parts of the triangle and how they interact with each other. By comprehending equilateral triangles, students can better understand other types of triangles and geometric shapes, leading to a better understanding of geometry.

Moreover, the real-life applications of equilateral triangles highlight the importance of this form of a triangle in various fields. Equilateral triangles provide stability and balance from construction to navigation, which is crucial for constructing efficient and accurate systems.

In addition, comprehending equilateral triangles can also help individuals appreciate the beauty of geometric shapes in art and architecture. The use of equilateral triangles in various forms of art and design demonstrates their significance in creating balance and symmetry.

In conclusion, understanding equilateral triangles is crucial not only for academic purposes but also for practical applications. It helps individuals develop critical thinking and problem-solving skills, appreciates the beauty of geometric shapes in art and architecture, and understand the significance of stability and balance in various fields. Therefore, it is essential to study and comprehend equilateral triangles in geometry.