Matrix Definition

A matrix is a rectangular array of numbers, symbols, or expressions, arranged in rows and columns. Matrices are widely used in mathematics, engineering, and science to represent data, perform calculations, and model real-world problems.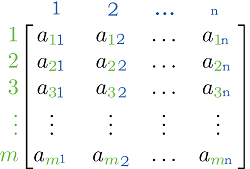

About matrix

Matrices are often denoted by capital letters, such as A, B, or C. The elements in a matrix are denoted by a lowercase letter with a subscript, such as aij, where i refers to the row and j refers to the column.

Properties of matrix

One important property of matrices is their size, which is defined by the number of rows and columns. A matrix with m rows and n columns is said to be an mxn matrix. If a matrix has the same number of rows and columns, it is called a square matrix.

Matrices can be added and subtracted element-wise, as long as the matrices being added or subtracted have the same size. In other words, to add or subtract two matrices, the elements in the corresponding positions are simply added or subtracted.

The product of two matrices is defined only if the number of columns in the first matrix is equal to the number of rows in the second matrix. In this case, the product of the two matrices is a new matrix, whose elements are the sums of the products of the elements in the corresponding row and column.

Types of matrix

One important type of matrix is the identity matrix, which is a square matrix with ones on the main diagonal and zeros elsewhere. The identity matrix is often denoted by the letter I, and it has the property that if it is multiplied by any other matrix, the result is the original matrix.

Another important type of matrix is the diagonal matrix, which is also a square matrix with the elements outside the main diagonal being zeros.

Transformation of matrix

Matrices can be transformed through various operations, such as transposition, inversion, and diagonalization. The transpose of a matrix is a new matrix that is formed by reflecting the original matrix over its main diagonal. In other words, the rows of the original matrix become the columns of the transposed matrix, and vice versa.

Inversion of matrix

Inversion is the process of finding a matrix that, when multiplied by the original matrix, gives the identity matrix. In other words, if A is a matrix and A^(-1) is its inverse, then A * A^(-1) = A^(-1) * A = I. Not all matrices have inverses, but if a matrix does have an inverse, it is unique.

Diagonalization

Diagonalization is the process of finding a diagonal matrix that is similar to the original matrix. This means that there exists an invertible matrix P such that P^(-1) * A * P = D, where D is a diagonal matrix. Diagonalization can be useful because it can simplify the calculation of eigenvalues and eigenvectors, which play a crucial role in many areas of mathematics, science, and engineering.

Eigenvalues and eigenvectors are special scalars and vectors associated with a matrix. An eigenvalue of a matrix A is a scalar λ such that Av = λv, where v is a non-zero vector called an eigenvector. The eigenvectors and eigenvalues of a matrix can be used to study the properties of linear transformations and to solve systems of linear equations.

Matrices are also used to represent linear transformations in linear algebra. A linear transformation is a function that maps vectors to vectors, preserving the properties of vector addition and scalar multiplication. The matrix representation of a linear transformation allows us to perform the transformation efficiently and effectively.

Application of matrices

Additionally, matrices have many applications in a variety of fields. In computer graphics, matrices are used to represent transformations such as rotations, translations, and scaling. In economics, matrices are used to model systems of linear equations that represent relationships between variables, such as supply and demand. In physics, matrices are used to represent physical quantities, such as position and momentum, and to describe the evolution of physical systems over time.

In statistics, matrices are used to represent data sets, where each row represents an observation and each column represents a variable. The techniques of principal component analysis and singular value decomposition are based on matrices, and are widely used in data analysis and data compression.

In control systems, matrices are used to model dynamic systems, such as mechanical systems, electrical circuits, and control systems. The state-space representation of a dynamic system is a set of linear differential equations that describe the evolution of the system over time, and matrices are used to represent the coefficients of these equations.

Matrices also play a crucial role in the solution of linear equations. Gaussian elimination and LU decomposition are two matrix-based methods for solving systems of linear equations, and they are widely used in engineering and science. The determinant of a matrix is a scalar that provides information about the invertibility of a matrix, and it is used in the calculation of the inverse of a matrix.

Conclusion

In conclusion, matrices are a fundamental tool in mathematics, and they have a wide range of applications in science, engineering, and technology. They are used to represent data, perform calculations, and model real-world problems, and their versatility and power make them an indispensable tool for anyone working in these fields.