Division Definition

Division is a fundamental arithmetic operation that involves splitting a quantity or a number into equal parts. It is one of the four basic mathematical operations, along with addition, subtraction, and multiplication. The division is used to find how many times a number, known as the divisor, goes into another number, known as the dividend. The result of division is known as the quotient.

In mathematical terms, the division is denoted by the symbol "�" or "/". The dividend is placed on top of the division sign, and the divisor is placed below it. For example, the expression 10 � 2 means that we want to divide 10 by 2. The number 10 is the dividend, and the number 2 is the divisor. The resulting quotient is 5.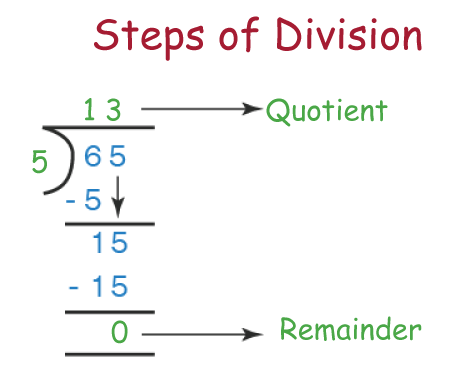

There are different methods of performing division, including long division, short division, and synthetic division. Each method has its advantages and disadvantages and is used in different contexts. However, the principles of division remain the same across all methods.

The concept of division is introduced to students in elementary school, typically in the second or third grade. At this level, the division is taught as repeated subtraction, where students learn to subtract the divisor from the dividend multiple times until they reach zero or a remainder. For example, to divide 10 by 2, students would subtract 2 from 10, then subtract 2 from the result, and so on until they reach zero or a remainder. The number of times they subtracted 2 would be the quotient.

As students progress through the grades, they learn more sophisticated methods of performing division, such as long division. Long division involves dividing the dividend by the divisor one digit at a time and placing the quotient above each digit. The process continues until the entire dividend has been divided, or until the remainder is zero or less than the divisor.

Different Forms of Division

• The short division is a simpler method of division that involves dividing the dividend by the divisor without showing the intermediate steps. This method is often used when the divisor is a small number or when the quotient is easy to calculate mentally.
• Synthetic division is a method of dividing polynomials, which are expressions that consist of a sum of terms, each term consisting of a variable raised to a power and a coefficient. Synthetic division involves dividing a polynomial by a linear factor of the form (x-a), where a is a constant. The resulting quotient is a polynomial of one degree less than the original polynomial.

In addition to the basic division operation, there are other related concepts that are important to understand. These include the remainder, the quotient rule, and the inverse operation of multiplication.

The remainder is the amount left over after division has been performed. For example, when we divide 10 by 3, the quotient is 3 with a remainder of 1. The remainder can be important in certain situations, such as when dealing with fractions or when dividing large numbers.

The quotient rule is a property of division that states that when we divide two numbers with the same base, we can subtract their exponents. For example, 5³�5² = 5^(3-2) = 5¹ = 5. This rule is often used when working with exponents and logarithms.

The inverse operation of multiplication is the operation that undoes multiplication. It is important to understand this concept because division and multiplication are inverse operations of each other. That is, when we divide a number by another number, we are essentially undoing the multiplication that was performed to get the original result. For example, if we know that 3 x 4 = 12, we can find that 12 � 4 = 3 or 12 � 3 = 4.

The division is a fundamental mathematical operation that involves dividing a quantity or number into equal parts. It is used in various contexts, such as in fractions, decimals, and percentages. The division is introduced to students at an early age and is taught through various methods, including repeated subtraction, long division, short division, and synthetic division. Understanding the concepts of the remainder, quotient rule, and inverse operation of multiplication is crucial when working with division.

Uses of Division

The division is used in everyday life, such as when calculating tips, dividing a pizza into equal slices, or determining how much money each person in a group should contribute to split a bill. It is also used in many fields, such as science, engineering, and finance, to solve complex problems and make informed decisions.

Conclusion

In science, the division is used to calculate ratios, rates, and proportions. For example, scientists may use division to calculate the ratio of the mass of an object to its volume, which is known as its density. In engineering, the division is used to calculate distances, speeds, and forces. For example, engineers may use division to determine the speed of a vehicle by dividing the distance traveled by the time it took to travel that distance. In finance, the division is used to calculate percentages, interest rates, and profits. For example, financial analysts may use division to calculate the profit margin of a company by dividing its net income by its revenue.