Equivalent Fractions Definition

Introduction

Fractions are a basic concept in mathematics used to represent a part or a portion of a whole thing or object. They are used to represent quantities that are not whole numbers, such as a half or a quarter of something. Fractions can be used in many practical applications, such as cooking, construction, and financial calculations.

Fractions are written as a ratio of two numbers, the numerator (top part) and the denominator (bottom part), separated by a fraction bar between the numbers. The numerator represents the part or portion of the whole we select to present, while the denominator is used to represent the total number of equal parts made by cutting the whole thing or object. For example, in the fraction 9/10, the numerator is 9, and the denominator is 10. This fraction represents nine out of ten equal parts or 9/10 of the whole object or thing.

Equivalent fractions are a critical aspect of fractions and represent fractions with the same value, even though they may be expressed differently. This article will provide us with a complete overview of equivalent fractions, including their history, definition, types, and applications.

History of Fractions

Fractions have a long and rich history that dates back to ancient civilizations. The concept of fractions was first developed to solve practical problems related to sharing and dividing goods and resources.

The Egyptians were one of the earliest civilizations to use fractions. They used a system based on unit fractions, which are fractions with a numerator of 1. For example, they represented 2/3 as the sum of two unit fractions: 1/2 + 1/6. They used these unit fractions in their everyday life, such as measuring land and dividing bread.

The Greeks were also interested in fractions, and they developed a more sophisticated system of fractions. They used a system of reciprocals. Reciprocal can be stated as a fraction in which the numerator and denominator are reversed or exchanged with each other. For example, the reciprocal of 5/7 is 7/5. They also used a symbol for zero, which allowed them to write fractions with a zero numerator, such as 0/5.

In Middle Ages, fractions were used extensively in commerce and trade. The Italians developed a system of common fractions, which are fractions with a common denominator. This made it easier to add and subtract fractions. They also developed the concept of mixed numbers, which can be defined as a sum of a whole number or complete object and a proper fraction.

In the 16th century, the Dutch mathematician Simon Stevin introduced decimal fractions, which are fractions whose denominator is expressed in the power of 10. This allowed for easier calculation of fractions and made it possible to represent fractions as decimals. Stevin also developed the concept of the "rule of three," which is a method for solving proportions using fractions.

In the 17th century, Blaise Pascal, a French mathematician, developed Pascal's triangle, which is a triangular arrangement of numbers used in combinatorics and probability theory. He also developed the concept of Pascal's theorem related to projective geometry.

In the 18th century, the Scottish mathematician Colin Maclaurin developed the concept of continued fractions, which are fractions in which the numerator and denominator are themselves fractions. Continued fractions have many interesting properties and are used in the study of number theory and analysis.

In the 19th century, the German mathematician Carl Friedrich Gauss developed the theory of modular arithmetic, which relates to the study of fractions and remainders. He also developed the concept of complex numbers, which are numbers of the form u + i.v, where u and v are real numbers, and i is the imaginary unit.

In the 20th century, fractions were studied in the context of abstract algebra and group theory. The concept of a field, which is a set of numbers with addition and multiplication operations, was developed. Fractions are a fundamental concept in fields, as they allow for the division of one number by another.

In conclusion, fractions have a long and fascinating history that has evolved over thousands of years. They have been used to solve practical problems related to sharing and dividing goods and resources, as well as in more abstract mathematical contexts. Fractions continue to be an important concept in mathematics and are studied in various fields, including number theory, analysis, and abstract algebra.

Introduction to Fractions

Before we dig into equivalent fractions, it is essential to have a solid understanding of fractions in general. A fraction is used to denote a part of a whole or a collection. For example, if we have a pizza or circle that has been divided into five equal slices, each slice represents 1/5th of the whole pizza.

The numerator of the fraction is used to represent the number of parts that we are considering, and the denominator is used to represent the total number of parts in which the whole thing and object have been divided. In the pizza or circular object example, the numerator would be 1, representing one slice of the pizza, and the denominator would be 5, representing the total number of slices.

Types of Fractions

There are several types of fractions, including proper fractions, improper fractions, mixed fractions, complex fractions, like fractions, unlike fractions, and Equivalent fractions. Each type of fraction has its own properties and characteristics, which are important to understand in order to use them effectively in mathematical calculations.

1. Proper Fractions:

A Proper fraction can be defined as a fraction in which the value of the numerator is less than the value of the denominator, i.e., numerator < denominator. These fractions represent a part or portion of a whole that is less than one. For example, 1/2, 3/4, and 5/8 are all proper fractions. Proper fractions can be written as decimals, but they will always be less than one.

2. Improper Fractions:

Improper fractions are fractions in which the value of the numerator is comparatively greater than or equal to the value of the denominator, i.e., numerator > or = denominator. These fractions represent a part or portion of a whole greater than one. For example, 5/3, 7/4, and 13/2 are all improper fractions. Improper fractions can be written in the form of mixed numbers, which are a combination of a whole number and a proper fraction.

3. Mixed Fractions:

Mixed numbers can be defined as the combination of a whole number and a proper fraction. These numbers are written as the whole number followed by a fraction, such as 3 1/2 or 5 3/4. Mixed fractions or numbers can be converted into improper fractions simply by multiplying the whole number by the denominator and, adding the numerator, then placing the result over the denominator.

4. Complex Fractions:

Complex fractions are fractions that contain one or more fractions in the numerator or denominator or in both the numerator and denominator. These fractions can also be called compound fractions. Complex fractions can be simplified by finding a common denominator and multiplying or dividing the numerator and denominator as necessary.

5. Like Fractions:

Like fractions can be defined as fractions in which the denominator of the multiple fractions is the same, they can be added and subtracted by simply adding or subtracting the numerators while keeping the denominator the same. For example, 1/3, 2/3, and 4/3 are all like fractions.

6. Unlike Fractions:

Unlike fractions, are fractions with different denominators. They cannot be added or subtracted until they are converted into like fractions. To convert unlike fractions into like fractions, we first have to find the least common multiple (LCM) of the denominators and multiply each fraction by the appropriate factor to make the denominators the same.

7. Equivalent Fractions:

Equivalent fractions can be defined as fractions in which the value of the numerator and the value of the denominator are different (but the resultant is the same), but they represent the same portion or part of an object or thing. To find equivalent fractions, we just have to divide or multiply the numerator and denominator by the same number. For example, 3/5 and 6/10 are equivalent fractions; we just have to multiply 3/5 by 2 in the numerator and in the denominator, resulting in 6/10, and so are 1/2 and 2/4.

Understanding the different types of fractions is important in order to perform mathematical operations correctly. For example, adding and subtracting fractions requires a common denominator, which can be found by identifying the least common multiple of the denominators. Multiplying and dividing fractions involves multiplying or dividing the numerators and denominators separately.

Equivalent Fractions Definition

Fractions are a way to represent a portion or a part of a whole thing or object. Equivalent fractions are fractions that have different numbers as the numerators and the denominators but represent the same portion (part) or the same value of the whole thing or object. In other words, equivalent fractions have different representations but are equal in value.

To understand equivalent fractions, it is important to understand what numerators and denominators are, the numerator is the number above the fraction line, and it represents the number of parts we are interested in. The denominator is the number below the fraction line, and it represents the total number of parts that make up the whole.

To get an equivalent fraction, we need to multiply or divide the numerator and the denominator by the same number, this is because multiplying or dividing the numerator and the denominator with the same number will not change or affect the resultant value of the fraction, but it will change its representation.

For example, if we want to find an equivalent fraction of 1/2, we can multiply both the numerator and the denominator by two (2). This will give us the fraction 2/4, which is equivalent to 1/2. Similarly, we can find an equivalent fraction of 1/3 by simply multiplying both the numerator and the denominator by 3. This will give us the fraction 3/9, which is equivalent to 1/3.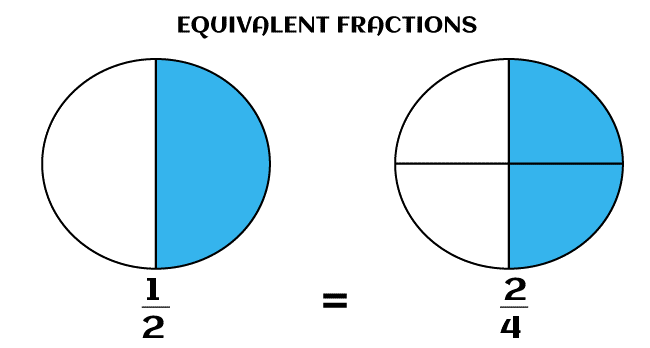

Parts of Equivalent Fractions

There are two parts of an equivalent fraction: the numerator and the denominator. The numerator is used to represent the number of parts that we are considering or presenting of the whole object, and the denominator is used to represent the total number of parts into which the whole object or thing has been divided.

To find if two fractions are equivalent, we can use the following method. We multiply the numerator of one (first) fraction by the denominator of the other (second) fraction and the denominator of the one fraction by the numerator of the other fraction. If we find that the results are the same, this implies that the fractions are equivalent.

For example, to determine if 1/3 and 2/6 are equivalent fractions, we would multiply 1 x 6 = 6 and 2 x 3 = 6. Since the results are the same, the fractions are equivalent.

Types of Equivalent Fractions

Equivalent fractions can be further classified into two types: simple and complex.

1. Simple Equivalent Fractions: Simple equivalent fractions are fractions in which only one fraction bar is present, i.e., a single fraction is there. For example, 1/3 and 2/6 are simple equivalent fractions because they can be simplified to 1/3 by dividing both the numerator and the denominator by 2.
2. Complex Equivalent Fractions: Complex equivalent fractions are fractions that have multiple fractions in their representation. For example, {[(1/2) x (1/4)] / [(3/8)]}, it can also be simplified to 1/3 when solved further.

Applications of Equivalent Fractions

Equivalent fractions have applications in different fields, including mathematics, science, engineering, and finance. Some of the common applications of equivalent fractions are as follows:

1. Arithmetic Operations: Equivalent fractions are very important in performing arithmetic operations on fractions, such as addition, subtraction, multiplication, and division. By expressing fractions in their simplest or equivalent form, we can compare and perform arithmetic operations on them more easily.
2. Scaling and Proportions: Equivalent fractions are used to represent the same portion of the whole in different contexts, i.e., different representations of the same fraction. For example, in scaling and proportion problems, equivalent fractions are used to determine the size of an object or a quantity of anything.
3. Ratios and Percentages: Equivalent fractions are used to represent ratios and percentages. For example, if a company has a market share of 25%, this can be expressed as a fraction of 1/4, which is an equivalent fraction.
4. Recipes and Cooking: Equivalent fractions are used in recipes and cooking to measure and mix ingredients accurately. For example, if any recipe asks for 1/2 cup of sugar, this can be expressed as 8 tablespoons or 24 teaspoons, which are all equivalent fractions.
5. Financial Calculations: Equivalent fractions are used in financial calculations, such as calculating interest rates, loan repayments, and discounts. For example, if a store offers a 20% discount on an item, this can be expressed as a fraction of 1/5, which is an equivalent fraction.

Conclusion

In conclusion, equivalent fractions are an important aspect of fractions and have different applications in several fields, including mathematics, science, engineering, and finance. Equivalent fractions represent fractions that have the same value, even though they may be expressed differently. Simple equivalent fractions can be simplified or reduced to their simplest form, while complex equivalent fractions can be simplified further. Equivalent fractions are used in arithmetic operations, scaling and proportion problems, ratios and percentages, recipes and cooking, and financial calculations. By understanding equivalent fractions, we can simplify fractions and perform arithmetic operations on them more easily.