Bulk Modulus DefinitionMeasurements and Definition of Bulk ModulusThe bulk modulus measures how stable an item is when compressed by external pressure. It makes use of the substance or material's flexibility. 
The items maintain their original sizes when external pressure is applied to a rigid solid substance. The total volume of all the item particles remains the same, even if it is broken into parts. However, the entire volume that an elastic item or substance occupies in the space decreases when such external pressure is applied to it. Bulk modulus addresses these elastic characteristics of materials. Another modulus, such as Young's, also provides the elastic properties of materials. The article defines bulk modulus in-depth and specifies the SI unit for bulk modulus. Elastic MaterialsWhen put under pressure from the outside, some materials resist destruction. These things or materials are referred to as elastic materials. An elastic material returns to its original form and size once the application of external pressure is stopped. Elasticity is the scientific name for this ability to withstand damage when not compressed. Several laws deal with elastic materials and describe and compute their elastic properties. These rules likewise determine their flexibility. Bulk modulus, shear modulus, Young's modulus, Hooke's law, etc., are such laws or formulas. The Bulk Modulus
K = Stress / Strain
CompressibilityThe computation of the bulk modulus provides a numerical measure of how incompressible the related substance or material is. As a result, the material's compressibility is determined by taking the inverse of the bulk modulus value. Bulk modulus and compressibility are inversely linked. As a result, a material's compressibility may be expressed as = 1 / K. Bulk Modulus EquationThe following equation displays the bulk modulus formula in accordance with the definition of the bulk modulus. K = Pressure on the material / Change in its volume K = Where,
The formula may be written as because external pressure causes the volume to decrease: K = K = -V ( The formula for calculating the bulk modulus while considering the density: K= ⍴ ( Where,
Bulk Modulus in SI units
The use of Bulk modulusThe following situations demonstrate how bulk modulus is used in daily life:
ConclusionManufacturing tires and weight-lifting ropes are only two examples of real-world applications where measuring the elasticity of the materials is required. The elastic materials continue to reshape and resize themselves even after being compressed externally. One may determine a material's elasticity by utilizing the idea of bulk modulus and its computation. The bulk modulus measures an elastic material's capacity for incompressibility. It is employed in liquid instances as well. It helps to determine a water body's pressure value based on its compressibility feature. The bulk modulus is discussed in the article, along with its SI unit. FAQs on Bulk Modulus1. Is the value of bulk modulus negative? Answer: The value of a substance's bulk modulus in an isothermal state is never negative. It's always a good thing. The bulk modulus formula's negative sign only shows a reduction in the substance or material's volume. 2. What does water's bulk modulus in numbers mean? Answer: Water has a bulk modulus of 2.15×109 Pa. 3. What does 'psi' in 'Bulk modulus' mean? Answer: Psi stands for pounds per square inch. According to the English system of units, it is the unit of bulk modulus. 4. What is the range of liquids' bulk modulus values? Answer: Most of the time, significant pressure is needed to compress liquids. As a result, liquids also have a high bulk modulus value. Typically, it lies between 2.50.000 to 3.000.000 psi. 5. What is implied when a liquid's bulk modulus is infinite? Answer: It implies that the material is the perfect liquid. It indicates that an endless amount of pressure is needed to compress a specific liquid.
Next TopicComplementary Angles Definition
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





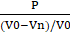
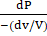
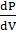 )
)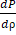 )
)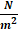 .
.




