Real Number Definition and Examples

History of Numbers

Don't you wonder, "How did early humans tally their things?" As we all have heard or read about, early humans crave marks on the walls of a cave by using stones, Charcoal, and bones to indicate their stories, and some of them even show patterns that resemble like Roman counting system to keep to keep a record of their things. Then in early civilizations (Greek, Egyptian, Aryans, etc.), they tried to write in a different way; they attempted to represent 'Numbers' in the form of objects- In the Ancient Egyptian counting system, a "coiled rope" is described as 100 and a "water lily" is represented as 1000, so by using symbols they represent Numbers. Then we started using positional notations to write down Numbers. By the end of the 7th Century, Indian Mathematics had developed a decimal or base ten positional system (0 to 9); by using this we can denote any real number with the use of only "ten unique symbols." As time passed away by Arabian merchants, scholars, and conquerors started to use this base ten positional system in Europe. We use these numbers today to denote word count and do mathematics and all our calculations.

Why are Numbers Used?

We have been listening to numbers since our childhood. Whenever we think about representing a count of something, we express it in 'numbers.' We think about counting money; we represent them in numbers, like '10,000$'. Numbers are very important in Mathematics, as everything in math is represented by numbers and letters. "So we can say that numbers are used as the notation of count of something, any object (like - Pages, Cars, Stars, etc.)."

Types of Numbers

There are two types of numbers:

1. Real Numbers
2. Imaginary or Complex Numbers

1.) Real Numbers: The numbers that exist in the real world and can be represented without the use of 'i-iota.' In proper we can say that real numbers are a set of collections of rational and irrational numbers (we will get more detail in the following explanations).

Ex: 1, pi, -2, 1.2345....., 2/3, 0, etc.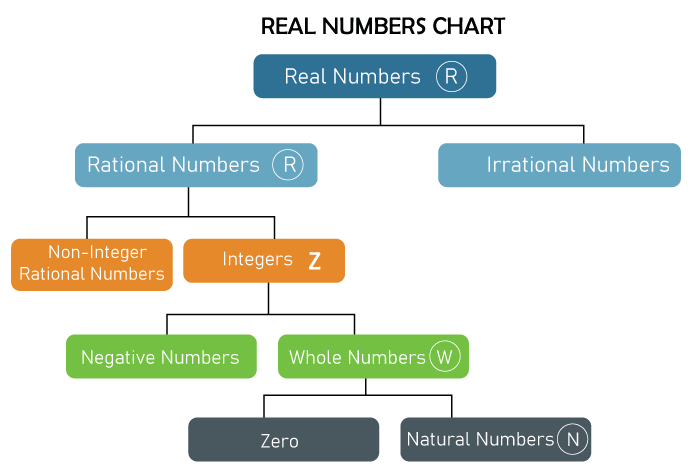

2.) Complex and Imaginary Numbers: The numbers that are represented with 'i-iota'. In particular, a 'Complex Number' is a set of collections of all real numbers, rational and irrational, with an iota (i).

Ex: 1+i, -2-i, 2/3+2i/3 etc.

Here We are talking about 'Real Numbers'

Real Numbers: Real Numbers can also be defined as a set of Natural Numbers, Whole Numbers, Integers Numbers, Rational Numbers, and Irrational Numbers and Real Numbers can be positive and negative; the Set of Real Numbers is characterized by "R." The Set of Positive Real Numbers is characterized by "R⁺". The Set of Negative Real Numbers is characterized by "R^-".

For Example: Let us consider 2, so we can write as "2 is a real number = 2 in R".

As mentioned above, a Real Number is a set of different subsets. As shown in the image given below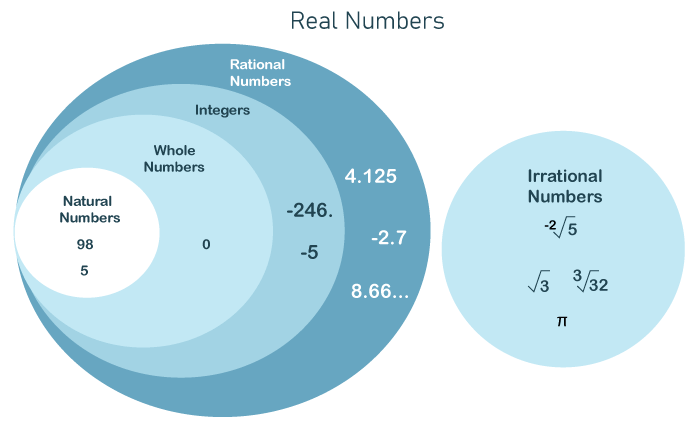

Let us talk about Natural numbers, Whole Numbers, Integer Numbers, Rational Numbers, and Irrational Numbers.

Natural Numbers: The set of numbers, which starts from 1 and continues to infinity is called Natural Numbers; all numbers are positive. The set of Natural Numbers is characterized by 'N.'

N = {1, 2, 3 ... infinity}

Whole Numbers: The set of Natural Numbers with a '0' number in it is called Whole Numbers; all numbers are positive. The Set of Whole Numbers is characterized by 'W.'

W = {0, 1, 2, 3... infinity}

Integer Numbers: The set of numbers from negative infinity to negative one, and Whole Numbers are Integer Numbers. This set is denoted by 'Z.' Set of positive Integer Numbers' Z⁺' and set of negative Integer Numbers' Z^-.'

Z = {- infinity... -3, -2, -1, 0, 1, 2, 3... infinity}

Z+ = {1, 2, 3... infinity}

Z- = {- infinity... -3, -2, -1}

Note: Zero is neither included in Z⁺ nor in Z^-, because zero (0) is neither positive nor negative.

Rational Numbers: The set of numbers that can be represented as a fraction of x and y, where 'x' and 'y' are integers and y is not equal to zero, are called Rational Numbers; where 'x' is called the "Numerator," and 'y' is called the "Denominator" in this fraction. Rational Numbers are also called terminating numbers because when the 'Numerator' is fully divided by the 'Denominator' with completion after the decimal. They are also positive and negative.

Q = {x/y: x, y in Z and y is not equal to 0}

Ex: Let us consider these numbers 1/5, 2, -5/4, 0, 4.25 etc.

Irrational Numbers: The set of numbers that are non-rational or cannot be represented in the form of fractions of x and y are called Irrational Numbers, In particular when the 'Numerator' is divided by 'Denominator' and the factor is not terminating even after many numbers after the decimal; also they are non-repeating in nature. The Set of Irrational Numbers is characterized by 'P" and they can also be positive and negative.

Ex: Consider, square -root of (2) = 1.414...

π=3.14......

As we can see in the above examples, these values cannot be represented as fractions of x and y. So they are Irrational Numbers.

Let us consider an example: 0.66666.....

As we can see that 0.6666 ...... = 1/3

It is non-terminable and repetitive in nature.

But it can be represented as a fraction of '1' and '3', so it is a Rational Number.

Representation of a Real Number on a Number Line

A Real Number can be represented on a "Real Line." A Real Line is used to determine the position of a 'number' in a plane or one dimension; every point on the Number Line represents a unique Real Number.

Step1.) Draw a horizontal straight line with arrows at the end of the line 'indicating opposite sides' and in the middle of the line, mark the number 0 as "O," where "O" is known as Origin.

Step2.) By writing numbers on the number line at a particular distance between them, on both sides of the Origin. Make sure the distance between the marked numbers is equal.

Step3.) Denote the Number on the Number Line by drawing a dot on the number line.

Ex: -3.6, -π/3, e, π etc

Types of Real Numbers on the Bases of Their Divisibility and Multiplicity

1. Prime Numbers
2. Even Numbers
3. Odd Numbers
4. Compound or Composite Numbers

1.) Prime Numbers: When a number is only divisible by one (1) and the number itself, that Number is called a Prime Number.

Ex: 2, 3, 5...

2.) Even Numbers: When a number is divisible by two (2), that number is called an Even Number.

Ex: 2, 4, 6...

3.) Odd Numbers: When a number is not divisible by two (2), that Number is called Odd Number.

Ex: 3, 5, 7, 9...

4.) Compound or Composite Numbers: When a number can be written in multiple of different numbers, or we can say they are opposite of prime numbers, that Number is called a Composite or Compound Number.

Ex: 8 = 2×4, 2×2×2, 1×8

14 = 2×7, 1×14

Properties of Real Numbers

There are mainly three properties of Real numbers, but we will discuss all the properties of Real Numbers.

Main three Properties:

1. Commutativity
2. Associativity
3. Distributivity

Other properties:

1. Closure
2. Existence of Identity element
3. Existence of Inverse element
4. Transitivity
5. Density
6. Order

Let us discuss all the properties one by one;

Commutativity: When we add and multiply two real numbers in different orders of their presentation, and the product is the same in both ways, they are commutative.

Ex: Let x and y in R

Then by property of commutativity

x + y = y + x and x × y = y × x

Associativity: When we add and multiply three real numbers in a different order and with brackets, and the products are the same in every way, they are associative.

Ex: Let x, y, and z in R

Then by property of Associativity

(x + y) + z = x + (y + z) and

(x × y) × z = x × (y × z)

Distributivity: When we multiply two numbers and then add them equal to adding them first and then multiplying them, we get the same result; this is called Distribution.

Ex: Let x, y, and z in R

Then by property of Distribution

x × (y + z) = x × y + x × z

(x + y) × z = x × z + y × z

Closure: When we add, multiply, Subtract, and divide any two real numbers, then the results will also give a real number; this property is called Closure.

Ex: 2 + 3 = 5, 2 and 3 in R, and 5 is also in R

Existence of Identity Element: There are two types of Identity elements

1. Additive Identity
2. Multiplicative Identity

a.) Additive Identity: A real number is called an additive Identity; when it is added to the number, it gives that same number as a result, '0' is called an Additive Identity.

Ex: a + 0 = a, a and 0 in R

b.) Multiplicative Identity: A real number is called multiplicative Identity; when it is multiplied by, it gives the same number as a result, '1' is called a Multiplicative Identity.

Existence of Inverse element: There are two types of Inverse elements

1. Additive Inverse
2. Multiplicative Inverse

a.) Additive Inverse: For every Real Number, there exists a unique number; when added to the number gives Additive Identity (0); that Number is called Additive Inverse.

Ex: a + (-a) = 0, a and (-a) in R

Here, (-a) is called Additive Inverse

b.) Multiplicative Inverse: For every Real Number, there exists a unique number; when multiplied by the Number gives multiplicative Identity (1), and that number is called Multiplicative Inverse.

Ex: a × (1/a) = 1, a in R and a is not equal to 0

Here, (1/a) is called Multiplicative Inverse.

Transitivity: When we think of a real number, there will always be many numbers smaller than and greater than that Number which we are thinking of; this property is called Transitivity.

Ex: Let us think of 19.

As, 18 < 19 < 20

Density: There are infinite real numbers in between any smallest number we can think of; this shows that real numbers are densely packed on the number line.

Ex: Let us think of 0.12 and 0.13

0.12 < 0.125 < 0.13

Order: Any two real numbers can be ordered by using < (less than), > (greater than), and = (equal to) signs.

Ex: Let x and y be in R

Either x > y and x < y or x = y

Some Important Points

• '0' is a unique number that is neither positive nor negative.
• One '1' is not a prime number because it is only divisible by one (1) and has only one factor.
• '2' is the only number that is 'even' and 'prime.'

Applications of Real Numbers

Real Numbers are used in every area of Mathematics, Physics, Engineering, and Economics. Some of them are given below

1. Computer Science: Real Numbers represent time, space and probability, etc., in Computer Science.
2. Statistics: Real Numbers are used to represent data and to calculate summary statistics such as mean, variance, and standard deviation.
3. Geometry: Real numbers are used to represent distances, angles, measurements, etc.
4. Calculus: Real numbers are used to describe the behavior of functions, calculate derivatives, and have definite integration.
5. Finance: Real numbers are used to represent monetary values and to calculate interest rates and other financial quantities.

Conclusion:

• Any Real Number can be represented using notations from' 0 to 9'.
• Real Numbers are very vast.
• Real Numbers can be represented on a Number Line.
• Every real Number is unique in itself.
• Real Numbers are used to representing tally objects, things, and money.
• Real Numbers are important in almost every field of Mathematics.

Let us do some exercises about what we have learned

Q1. What is the definition of a Real Number?

Answer: Real Number is a collection of rational and irrational numbers; it is denoted by 'R'.

Q2. Is zero '0' a positive number?

Answer: No, zero is neither positive nor negative. Because '0' is located in the middle of a number line.

Q3. Who discovers the notation of '0'?

Answer: Famous Mathematician 'Aryabhata' discovered the notation of zero.

Q4. What is an even prime number?

Answer: The real Number which is even and prime is called an even prime Number. There is only '2' which satisfies this category.

Q5. Can we write the largest number in the Real number system?

Answer: No, writing the largest real Number is impossible due to the 'transitivity' of real numbers.

Q6. Is the real Number one '1' prime Number?

Answer: No, 1 is not a prime Number. Because the prime number is only divisible by one and itself, two factors must be there, but in the case of 1, there is only one factor.