KVL Definition

Circuit analysis is based on Kirchhoff's circuit laws. These rules, along with the equation for each component (resistor, capacitor, and inductor), give us the fundamentals we need to begin analyzing circuits. In this article we are going to cover the Kirchhoff current and voltage laws and their application to circuit analysis.

Kirchhoff's Circuit rules provide a framework for creating a set of fundamental network rules and theorems for the voltages and currents within a circuit, allowing us to address challenging circuit problems. In this article we will be covering KVL (Kirchhoff's Law) in detail.

Gustav Robert Kirchhoff

Before beginning on to the main article, let us take a background check about Gustav Robert Kirchhoff. On March 12, 1824, in Konigsberg, Prussia, a German scientist named Gustav Robert Kirchhoff was born. The conduction of electricity was his initial area of study. The Laws of Closed Electric Circuits were developed by Kirchhoff in 1845 as a result of his studies.

Kirchhoff's Voltage and Current Laws are the current names for these laws, which were finally given his name. Understanding the principles of these laws, which govern all electric circuits, is essential to comprehending how an electronic circuit works. Although Kirchhoff is forever known in electrical engineering because of these laws, he made other important discoveries as well.

The fact that an electrical impulse moved at the speed of light was first independently verified by him. Kirchhoff also expanded the study of blackbody radiation and made a significant contribution to spectroscopic research.

What are Kirchhoff's Laws?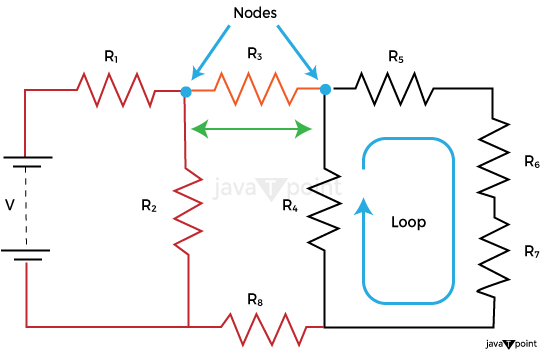

The principles governing the conservation of current and energy in electrical circuits were created by German physicist Gustav Kirchhoff in 1845. Kirchhoff's Voltage and Current Law is the name given to these two laws in most contexts. These rules make it easier to determine a complicated network's electrical resistance, or impedance in the case of an AC network, as well as the current flow through various network streams.

Kirchhoff's first law - Current Law - (KCL)

Kirchhoff's Current Law is also known as Kirchhoff's First Law and Kirchhoff's Junction Rule. The Junction Rule asserts that the total current in a circuit, including within and outside of junctions, is equal.

Kirchhoff's second law - Voltage Law (KVL)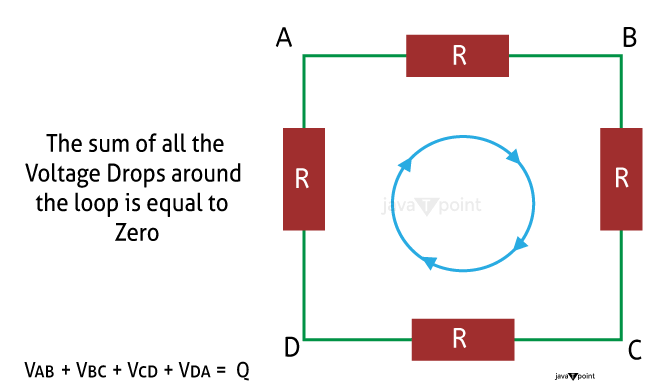

Kirchhoff's Voltage Law is also known as Kirchhoff's Second Law and Kirchhoff's Loop Rule. According to the "loop rule," a closed loop's surrounding voltages add up to zero.

According to Kirchhoff's Voltage Law (KVL), "In any closed loop network, the total voltage around the loop is equal to the sum of all the voltage drops within the same loop," which is also equal to zero. In other words, all of the voltages inside the loop's algebraic total must be zero. Kirchhoff's theory is referred to as the Conservation of Energy.

Why Kirchhoff's laws is Needed

Kirchhoff's circuit law in relation to the junction rule and his closed loop rule can be used to compute and determine the currents and voltages around any closed circuit, provided we are aware of the values of the electrical components inside it. We know that, when two or more resistors are linked in series, parallel, or a mix of the two, a single equivalent resistance, or R_T, can be found, and these circuits follow Ohm's Law.

However, there are situations when we cannot just utilize Ohm's Law alone to identify the voltages or currents flowing within the circuit, such as in bridge or T networks. Kirchhoff's Circuit Law can be used to provide the guidelines that enable us to acquire the circuit equations for these kinds of calculations.

Kirchhoff's Voltage Law (KVL)

Starting at any point in the loop, go in the same way while taking note of the direction in which every voltage drop, whether positive or negative, occurs, and then go back to where you started. In order for the ultimate voltage sum to equal zero, the direction must remain constant, whether it be clockwise or anti-clockwise. When investigating series circuits, we can apply Kirchhoff's voltage law.

Kirchhoff's Circuit Laws are used to analyse both DC and AC circuits, and a number of terminology and terminologies are used to characterise the circuit elements that are being analysed, including nodes, routes, branches, loops, and meshes. It is crucial to comprehend these concepts because they are commonly used in circuit analysis.

Common DC Circuit Theory Terms

Circuit - A closed loop conducting path in which an electrical current flows is referred to as a circuit.

Path - A path is a single connection between two sources or constituents.

Node - A node is a junction, connector, or terminal in a circuit when two or more circuit components are connected or joined together to provide a connection point between two or more branches. A dot designates a node.

Branch - A branch is a component or collection of components, such as a resistor or a source, that connects two nodes.

Loop - A loop is a straightforward, closed path in a circuit where no circuit component or node appears more than once.

Mesh - A mesh is a closed loop series path that is a single path only and does not contain any other paths. A mesh doesn't contain loops.

Two important points to remember:

(I) If the same amount of current runs through all of the components, they are said to be connected into series.

(II) If the same voltage is delivered across multiple components, they are said to be connected in parallel.

Applications of Kirchhoffs Circuit Laws:

Kirchhoff's Circuit Laws are used in the following way to find the currents and voltages in a circuit, which is referred to as "analysing" the circuit:

1. Assume that all resistances and voltages are known. If not, write V1, V2, R1, R2, etc. on them.
2. Distributes a current (clockwise or anticlockwise) to each branch or mesh.
3. >3. Add a branch current to each branch. ( I1, I2, I3 etc. )
4. Find the equations for each node's Kirchhoff's first law.
5. Determine the Kirchhoff's second law equations for each of the circuit's independent loops.
6. Use linear simultaneous equations to find the elusive currents as needed.

As well as using Kirchhoff's Circuit Law to calculate the various voltages and currents cycling around a linear circuit, we can also utilise loop analysis to determine the currents in each independent loop which, helps to reduce the amount of mathematics necessary by using simply Kirchhoff's rules.

Frequently Asked Questions (FAQs)

Q.) State Kirchhoff's Current Law

Ans.) Kirchhoff's Current Law states that the total current entering a junction or a node matches the charge exiting the node as no charge is lost.

Q.) What is Kirchhoff's First Law also known as?

Ans.) Kirchhoff's First Law is also known as Kirchhoff's Current Law.

Q.) Describe the Kirchhoff voltage law.

Ans.) According to Kirchhoff's voltage law, for any closed network, the voltage around a loop is equal to the sum of all voltage drops in that loop and is equal to zero.

Q.) Who put forth Kirchhoff's laws?

Ans.) Kirchhoff's laws were put out by Gustav Robert Kirchhoff

Q.) Kirchhoff's second law is also known as?

Ans.) Kirchhoff's voltage law is another name for Kirchhoff's second law.

Kirchhoff's Law Solved Examples

Question:

If R₁ = 2?, R₂ = 4?, R₃ = 6?, determine the electric current that flows in the circuit below.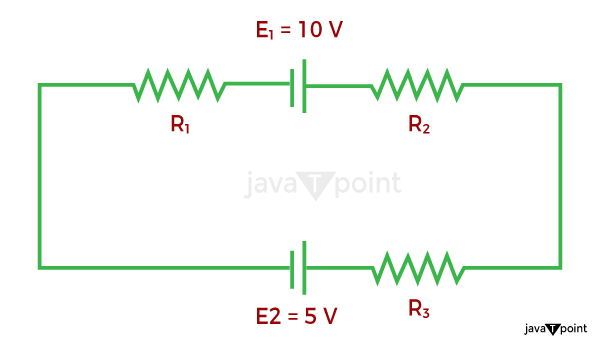

Solution:

The following considerations should be made as you approach the issue:

The current direction must be determined. Let's choose the clockwise path for this issue.

A potential decrease occurs when the current flows across the resistor. As a result, V = IR has a negative sign.

The emf (E) source is positive if the current changes from low to high because the emf source is charged with energy. The source of emf (E) is also indicated negatively if the current changes from high to low voltage (+ to -), as a result of energy being expelled from the emf source.

In this solution, the current flows in the same direction as the clockwise direction of rotation.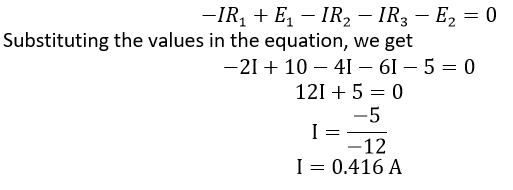

The circuit has a 0.416 A electric current flows through it. Since the electric current is a positive sign, it flows in the same clockwise direction as the direction of rotation. The direction of the current would be anticlockwise if the electric current was negative.