Circumference Definition

Introduction:

Once upon a time, Raju and his parents went on summer vacation. During his summer vacation, he was not able to identify some figures that were present in the park. There are numerous types of shapes and figures present in the park. Raju asks his parents about the figures. And his parents explain every figure one by one. As we already know, numerous types of shapes and figures are present in current times. And these figures Rae studied in the various branches of mathematics. Some of the most notable figures include circles, squares, rectangles, etc.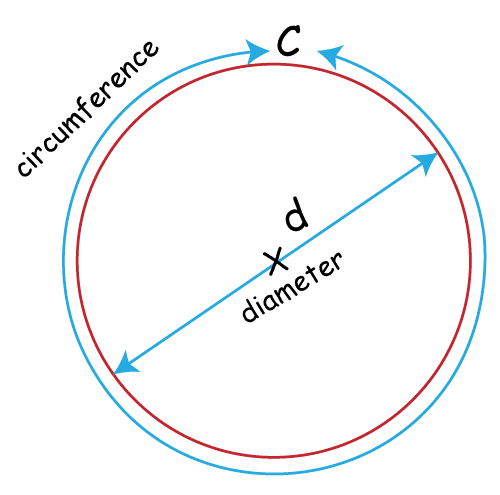

Let us try to understand some of the common mathematical figures. In mathematics, everything starts with the point. A point is defined as a location in space that does not have any size or dimensions. Dot is used to represent the point.

A line is an important figure in mathematics. It is drawn between two points. It is considered a straight path that may be extended infinitely in both directions. A straight line with two arrowheads usually represents it. An angle is the measure of the space drawn between two intersecting lines. Angel measured in degrees. A triangle is another important figure in mathematics. It is considered a three-sided polygon. The triangle can be classified into numerous types based on the length of its sides and the measure of its angles. The circle is considered one of the most notable figures in mathematics; it helps to understand different mathematics-related theories effectively. The circle is a round shape figure that has a constant radius. It is defined as the set of all points in a plane equidistant from a given point called the center. Some of the other important figures of mathematics include rectangles, squares, cylinders, cubes, spheres, etc. In the article, we will discuss the circle and its related concepts.

What is Circumference?

A circumference is an actual distance around the boundary of a circular object. Circumference is also considered as distance in curved geometric figures. Circumference measures the total length of the boundary drawn on a circular figure or over a curved figure. Circumference is calculated by the formula C = 2?r, where C is the Circumference, r is the radius, and ? (pi) is a mathematical constant approximately equal to 3.14159. Circumference is also calculated using the formula C = ?d, where d is the circle's diameter. A circle and its Circumference are considered an important measurement in geometry. Because it is used in many real-world applications, such as calculating the distance around a circular track or the length of wire needed to wrap around a circular object. Circumference is a very important concept in mathematics. It helps to understand the parameters of some other figures. The value of pi is discovered by various theories and proof of the theorem. Pi and the Circumference of a circle are interrelated to each other.

Features of Circumference:

There are numerous types of features that are used to donate the Circumference of circular figures.

Here are some features of the Circumference:

1. The most important feature of the Circumference is that it is considered as the measure of the total length of the boundary of a circle.
2. Circumference is related to radius by the formula C = 2?r. Also, Circumference is directly proportional to the diameter of the circle.
3. Circumference has various usages, mainly in mathematical calculations and real-world applications. It is an important figure in parameter geometry.
4. The Circumference of a circle is a transcendental number. It means it cannot be expressed exactly or fixed as a finite decimal or fraction.
5. The value of pi (?) is a mathematical constant used to represent the ratio of the Circumference of a circle to its diameter. The value of pi is approximately equal to 3.14159.
6. The Circumference of a circle can be used to calculate other parameters of a circle, such as its area, diameter, and radius.
7. It is a continuous curve with no sharp corners or edges.
8. It can be measured using a flexible measuring tape or mathematical formulas.

Apart from these chief characteristics, numerous other features help to understand the Circumference of the circle and how it is different from other proofs and concepts.

Characteristics of Circumference:

As in the above paragraphs, we discussed the definition of Circumference and some of its features. We know that Circumference is a geometric shape that consists of all points in a plane that are equidistant from a fixed point called the center. Some of the characteristics of a circumference include:

Diameter:

The diameter is the line segment that usually passes through the circle center with endpoints on the Circumference. It is equal to twice the length of the radius.

Radius:

Radius is the distance between any point on the Circumference and the circle's center. It is half the length of the diameter.

Circumference length:

Distance around the circle is defined as the circumference length. It is equal to 2? times the radius or ? times the diameter.

Area:

The area of the circle is defined as the amount of space occupied by the Circumference, and it is usually equal to the ? times the square of the radius. The area is 1/4 times the square of the diameter.

Chord:

A line segment used to connect two points on the circle's Circumference is defined as a chord.

Tangent:

The line intersecting the Circumference at the fixed point is known as a tangent.

Arc:

The portion between the two points on the Circumference is termed an arc.

These are the characteristics of Circumference. These characteristics are fundamental to studying and understanding circles and their applications in mathematics, science, and engineering.

Usage of Circumference:

The concept of Circumference has a very wide application, and it is used in various fields; some of the most notable applications include:

Geometry:

Geometry is one of the most important branches of mathematics. Everything is directly or indirectly related to geometry. Geometry has wide applications, from designing a small object to a large infrastructure that needs geometry. Circles are regarded as one of the most notable and fundamental shapes in geometry. They are essential in the field of geometry. Circumference and its related concepts are very important in the study of geometry. Some very serious geometrical problems are solved by using formulas related to the Circumference of a circle, such as finding the area or Circumference of a circle. They can be solved using formulas that are based on the Circumference.

Engineering:

Due to changes in needs and consumer demand, those products have attractive designs. Circles and their corresponding figures are used in various fields of engineering. They are used to design gears, pulleys, and wheels. With the Circumference of a circle calculation, it is crucial to calculate the speed and distance traveled by these objects. Hence Circumference has. Very wide application in engineering by providing formulas to calculate the working of objects.

Navigation:

The most remarkable usage of the Circumference of the Circle is that it helps in navigation and surveillance. Earth circumference is used to navigate the pat. Cartography, with the help of Circumference, is used to calculate distances, determine the size of areas, and create accurate maps.

Astronomy:

Circumference has a very wide application. It is used in astronomy to calculate the size and distance of celestial objects. For instance, the Circumference of a planet, a star, or any celestial body can be calculated by observing its angular size and using the principles of trigonometry. Astronomy is essential to predict future events. Understanding these circumferences is very beneficial for science.

Sports:

As there are numerous types of sports played worldwide. The requirement for a ball in different sports is different. Circumference helps to develop balls of different sizes. The Circumference of a ball is essential in various sports. Most importantly, in basketball, soccer, and volleyball, the size of the ball is crucial. The size of the ball and the Circumference affect the game's dynamics, such as the way the ball bounces and how players handle it. So with the help of Circumference and its related concepts, we can develop different types of balls and other sports requirements.

Conclusion:

In the above paragraphs, we discussed the definition of Circumference, its features, and its characteristics. It has very wide applications. Apart from mathematics, it is used in numerous other fields. Understanding this concept is crucial to solving problems in mathematics, science, and engineering problems.