Computer Science Quiz - III: Part 1

Topic - 6 Data Structures

1) Arrays A and B are to be used to store two matrices, M1 and M2, respectively. Each array can be placed in adjacent memory regions either in row-major order or in column-major order. An algorithm's computational complexity in terms of time to compute M1 x M2 is

Best if one of them is stored in row-major and the other in column-major
Best if both are stored in row-major order
Best if both are stored in column-major
No dependencies on the storage scheme

Answer: (d) No dependencies on the storage scheme

Explanation: Note that the issue concerns time complexity rather than actual program execution time. No matter how we store array members, we must always access the same number of M1 and M2 elements in order to multiply the matrices in terms of time complexity. When performing element access in arrays, the time complexity is always constant or O(1); the constants may change for other methods.

2) Which is the most effective data structure to use when determining whether the parenthesis in an arithmetic expression is balanced?

AVL Tree
Binary Tree
Queue
Stack

Answer: (d) Stack

Explanation: Stack is the most effective data structure to use when determining whether the parenthesis in an arithmetic expression is balanced

3) Which statement regarding the linked list implementation of the stack is accurate?

I. If new nodes are added to the beginning of a linked list during a push operation, nodes must be removed from the end during a pop operation.

II. If new nodes are added at the end of a push operation, the beginning nodes must be deleted during a pop operation.

Both I and II
I only
II only
Neither I nor II

Answer: (d) Neither I nor II

Explanation:

The stack data structure follows first in, last out policy.

In the linked list implementation of stack, if the node is added at the beginning of the list during a push operation, then the node must be removed from the beginning of the list during a pop operation. Or if the node is added at the end of the list during a push operation, then the node must be removed from the end of the list during a pop operation.

The above statements are true for the queue data structure.

Therefore, (d) is the correct answer.

4) On a stack, the following sequence of tasks is carried out.

PUSH (10), PUSH (13), PUSH (43), POP (), POP (), PUSH (76), PUSH (7), POP (), PUSH (90), PUSH (24), POP (), POP (), POP (), POP ()

The order in which the values were poped is

10, 13, 43, 76, 7, 90, 24
43, 13, 7, 24, 90, 76, 10
24, 90, 7, 76, 43, 13, 10
43, 13, 10, 7, 76, 24, 90

Answer: (b) 43, 13, 7, 24, 90, 76, 10

Explanation: Stack data structure follows last in first out policy i.e., the newly added element (top of the stack) will be removed first

Each step is explained in the table below:

Operation	Stack	Output	Explanation
PUSH (10)	[10]	-
PUSH (13)	[10, 13]	-
PUSH (43)	[10, 13, 43]	-
POP ()	[10, 13]	[43]	The top element of the stack was 43.
POP ()	[10]	[43, 13]	The top element of the stack was 13
PUSH (76)	[10, 76]	[43, 13]
PUSH (7)	[10, 76, 7]	[43, 13]
POP ()	[10, 76]	[43, 13, 7]	The top element of the stack was 7.
PUSH (90)	[10, 76, 90]
PUSH (24)	[10, 76, 90, 24]
POP ()	[10, 76, 90]	[43, 13, 7, 24]	The top element of the stack was 24.
POP ()	[10, 76]	[43, 13, 7, 24, 90]	The top element of the stack was 90.
POP ()	[10]	[43, 13, 7, 24, 90, 76]	The top element of the stack was 76.
POP ()	-	[43, 13, 7, 24, 90, 76, 10]	The top element of the stack was 10.

The output Sequence would be [43, 10, 7, 24, 90, 76, 10]. Hence, (b) is the correct answer.

5) 5 On a queue, the following sequence of tasks is carried out.

ENQUEUE (9), ENQUEUE (3), DEQUEUE (), ENQUEUE (17), ENQUEUE (25), DEQUEUE (), DEQUEUE (), ENQUEUE (16), DEQUEUE (), DEQUEUE ()

The order in which the values were dequeued is

3, 25, 17, 16, 9
16, 25, 17, 3, 9
9, 3, 17, 25, 16
3, 9, 25, 17, 16

Answer: (c) 9, 3, 17, 25, 16

Explanation:

Queue data structure follows first in first out policy. Element inserted first (Front of the queue) will be removed first.

Each step is explained in the table below:

Operation	Queue	Output	Explanation
ENQUEUE (9)	[9]	-
ENQUEUE (3)	[9, 3]	-
DEQUEUE ()	[3]	[9]	9 was the first to be inserted.
ENQUEUE (17)	[3, 17]	[9]
ENQUEUE (25)	[3, 17, 25]	[9]
DEQUEUE ()	[17, 25]	[9, 3]	3 was inserted before 17 and 25.
DEQUEUE ()	[25]	[9, 3, 17]	17 was inserted before 25.
ENQUEUE (16)	[25, 16]	[9, 3, 17]
DEQUEUE ()	[16]	[9, 3, 17, 25]	25 was inserted before 16.
DEQUEUE ()	[]	[9, 3, 17, 25, 16]	16 was the last element.

The output Sequence would be [9, 3, 17, 25, 16]. Hence, (c) is the correct answer.

6) Evaluate the postfix expression for the given infix expression:

A + B * C - (F + D) + E / G - H

ABC*+FD+-EG+/H-
ABC*+FD+-EG/-H+
ABC*+FD+-EG/+H-
ABC*+FD-+EG/-H+

Answer: (c) ABC*+FD+-EG/+H-

Explanation:

The stepwise conversion of infix to postfix is given in the form of the table below:

Incoming Symbol	Operation	Stack	Postfix Expression	Reason
A		Null	A
+	Push (+)	+	A
B		+	AB
*	Push (*)	* +	AB	* has high precedence then +.
C		* +	ABC
-	Pop () Pop () Push (-)	-	ABC*+	- has low precedence then * that's we popped and + and - follows left to right associativity that's + is also popped
(	Push (()	( -	ABC*+
F		( -	ABC*+F
+	Push (+)	+ ( -	ABC*+F	+ has low precedence than '(' that's why we pushed it.
D		+ ( -	ABC*+FD
)	Pop () Pop ()	-	ABC*+FD+	As soon as we get ')', we must pop until we encounter '('.
+	Pop () Push (+)	+	ABC*+FD+-	+ and - has the same precedence. And follows left-to-right associativity. That's why we popped '-' and pushed '+'
E		+	ABC*+FD+-E
/	Push (/)	/ +	ABC*+FD+-E	/ has high precedence
G		/ +	ABC*+FD+-EG
-	Pop () Pop () Push (-)	-	ABC*+FD+-EG/+	- has low precedence than /, and + came first that's why we popped both.
H		-	ABC*+FD+-EG/-H
NULL	Pop ()	NULL	ABC*+FD+-EG/-H-

The postfix expression obtained is ABC*+FD+-EG/-H-. Hence, (c) is the correct answer.

To learn the conversion of expression from one notation to another, please follow the given link:

https://www.javatpoint.com/convert-infix-to-postfix-notation

7) What is the output of the following function for the number if 484 is passed to it?

bool YOO (int n)

{

int x = 0;

for (int odd = 1; n > x; odd = odd + 2)

x = x + odd;

return (n == x);

}

What is its general purpose?

Ture, Checks whether the given number is even or not
False, Checks whether the given number is divisible by 4 or not
False, It does nothing
True, Checks whether the input is a perfect square or not

Answer: (d) True, Checks whether the input is a perfect square or not

Explanation: The provided function adds each odd number (1, 3, 5, 7, 9, .........., so on) until the total is less than or equal to n. The function returns true if the sum equals n. In a sense, this is a test for exact square numbers. The sum of odd numbers can be used to represent any perfect square number. For example:

1 = 1

4 = 1 + 3

9 = 1 + 3 + 5

16 = 1 + 3 + 5 + 7

484 can be written as 1 + 3 + 5 + 7 + 9 + 11 + ..... + 47.

8) Which of the following is a queue data structure application?

When several consumers share a single resource.
When information is exchanged asynchronously (information is not always received at the same rate as it is sent) between two processes.
Load balancing,
All of the above

Answer: (d) All of the above

Explanation:

a. When multiple consumers share the same resource. CPU scheduling and disc scheduling are two examples.

b. When information is exchanged between processes asynchronously (information is not always received at the same pace as it is sent). Examples include pipelines and IO Buffers.

c. Message loading can be balanced or distributed among several adapter services thanks to load balancing using the distributed queue. Load balancing reduces stress failures and makes sure no single service is overloaded. By avoiding a single point of failure, it additionally enables fault tolerance. Both the incoming and outbound sides of the adapter arrangement can operate in load-balanced configurations.

Therefore, (d) is the correct answer.

9) Which statement regarding the linked list implementation of the Queue is accurate?

I. If new nodes are added to the beginning of a linked list during an Enqueue operation, nodes must be removed from the end during a dequeue operation.

II. If new nodes are added at the end of an enqueue operation, the beginning nodes must be deleted during a dequeue operation.

I only
II only
Both I and II
Neither I nor II

Answer: (c) Both I and II

Explanation:

The queue data structure follows the first-in, first-out policy.

In the linked list implementation of queue, if the node is added at the beginning of the list during an enqueue operation, then the node must be removed from the end of the list during a dequeue operation. Or if the node is added at the end of the list during an enqueue operation, then the node must be removed from the beginning of the list during a dequeue operation.

The above statements are 100% true for the queue data structure.

Therefore, (c) is the correct answer.

10) Consider a queue is represented using a circular linked list. A pointer p is used to access the elements of the queue. Which node should p point to in order to allow for the constant-time execution of both the enQueue and deQueue operations?

Front Node
Rear Node
Middle Node
Minimum two pointers are required

Answer: (b) Rear Node

Explanation:

The given figure represents the same idea mentioned in the question.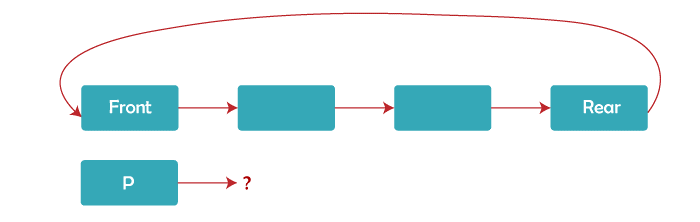

When 'p' points to the rear node, we can perform the enQueue and deQueue operations in constant time or O(1).

Suppose we have a new node (N).

To perform enQueue at the rear end, we make N -> next = p -> next

and change p -> next = N. This can be done in constant time and

To perform deQueue at the front, we make p -> next = p -> next -> next. The front node will be deleted by this method and can be achieved in constant time.

Hence, (a) is the correct answer.

11) An array of size n is used to implement a circular queue. Suppose the enQueue and deQueue operation is carried out at the rear and front end of the array, respectively. Also, the rear and front both were equal to zero initially. Identify the condition to detect the queue full and empty condition.

Full: Rear + 1 == n; Empty: Front == 0
Full: (Rear + 1) mod n == Front; Empty: Front == 0
Full: (Rear + 1) mod n == Front; Empty: (Front + 1) mod n == rear
Full: (Rear + 1) mod n == Front; Empty: Front == Rear

Answer: (d) Full: (Rear + 1) mod n == Front; Empty: Front == Rear

Explanation:

When a circular queue is implemented using an array, the condition to detect the queue full is (Rear + 1 mod n = Front) and to detect the queue empty is Front == Rear. There are two situations in which the queue is full:

I: When the Rear is before the Front i.e., Rear + 1 = Front:

(Rear + 1) mod n gives the front index.

II: When Rear == n - 1 and Front == 0

Rear + 1 becomes equal to n, and (Rear + 1) mod n == n mod n == 0 == Front.

Option (d) satisfies both conditions. Therefore, it is the correct answer.

The first option can be valid when the queue is not circular.

12) Consider a scenario where each set is represented as a linked list, with the entries appearing in any order. What procedure involving the union, intersection, membership, and cardinality will be the slowest?

Union and Intersection
Membership and Union
Cardinality and Intersection
Intersection only

Answer: (c) Union and Intersection

Explanation:

To find the Union of two sets - Consider two sets, A and B, represented using linked lists. For each element of A, we must compare each element in B. So, the time complexity to finding the union of two sets is O (m * n), where m and n are the cardinalities of sets A and B.
To find the Intersection of two sets - Here also, we must compare each element of A with every element in B. So, the time complexity to finding the intersection of two sets is O (m * n)
To find the Cardinality of a set - we only have to traverse the list once. So, the time complexity becomes O (n).
To find the membership - Here also, we only need to compare the given element with each element of the set, and in the worst case, it will take n comparisons. So, the time complexity becomes O (n).

Hence, (a) is the correct answer.

13) Which of the following operations is reliant on the length of the linked list if you are only provided pointers to the first and last nodes of a singly linked list?

Deleting the first node of the list
Deleting the last node of the list
Adding a new node as the first node
Adding a new node at the end of the list

Answer: (b) Deleting the last node of the list

Explanation:

Deleting the first node can be done in constant time by simply making the head pointer point to the second node.
Deleting the last node depends on the length of the list. To delete the last node, we must have access to the second last node; for that, we must traverse the whole list and make the last pointer point to the second last node and the next pointer null.
Adding a new node as the first node can be done in constant time. By making the next pointer of the node point to the head node and changing the head pointer point to the new node.
Adding a new node at the last node can be easily done in constant time by making the next pointer point to the new node and the last pointer point to the new node.

Hence, (b) is the correct answer.

14) The maximum number of edges in any root-to-leaf path determines the height of a binary tree. The maximum number of node nodes there can be in a binary tree of height h are:

2^h - 1
2^h + 1
2^{h + 1} + 1
2^{h + 1} - 1

Answer: (d) 2^{h + 1} - 1

Explanation: A tree is said to be a binary tree; each node in the tree can maximum have two children. The maximum number of nodes of a binary tree can be determined using 2^{h + 1} - 1.

Hence, (d) is the correct answer.

15) The longest root-to-leaf path in a tree determines its height. A binary tree of height 10 has a maximum and minimum number of nodes that are, respectively

1024 and 10
1023 and 11
2048 and 10
2047 and 11

Answer: (d) 2047 and 11

Explanation:

The maximum number of nodes of a binary tree can be determined using 2^{h + 1} - 1.

Maximum nodes = 2^{h + 1} - 1 = 2^{10 + 1} - 1 = 2048 - 1 = 2047

The minimum number of nodes of a binary tree can be determined using n + 1.

Minimum nodes = n + 1 = 10 + 1 = 11

Therefore, (d) is the correct answer.

16) Consider a binary tree with 63 nodes in it. The minimum and maximum height of the tree can be:

62 and 6
62 and 5
6 and 5
63 and 5

Answer: (b) 62 and 5

Explanation:

The relationship between the maximum height and nodes of a binary tree is

n = h + 1.

63 = h + 1

h = 63 - 1 = 62

The relationship between the minimum height and nodes of a binary tree is

n = 2^{h + 1} - 1.

63 = 2^{h + 1} - 1 => 63 + 1 = 2^{h + 1}

64 = 2^{h + 1}

2⁶ = 2^{h + 1}

6 = h + 1

h = 6 - 1 = 5

Therefore, (b) is the correct answer.

17) Consider a binary tree shown in the figure if the nodes are traversed in pre-order, in-order and post-order. Which of the following option is correct?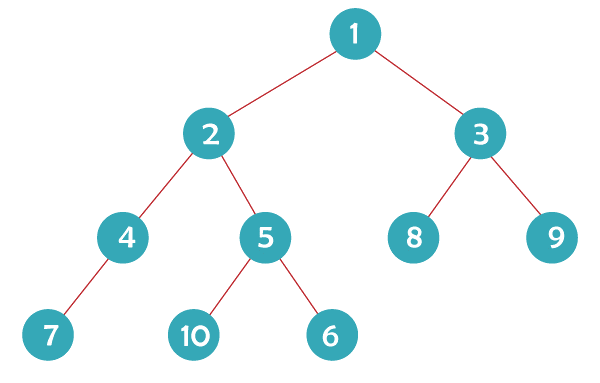

Pre-order: 1, 2, 4, 7, 5, 10, 6, 3, 8, 9
In-order: 1, 2, 3, 4, 5, 8, 9, 7, 10, 6
Post-order: 7, 4, 10, 6, 5, 2, 8, 9, 3, 1
Pre-order: 1, 2, 4, 7, 5, 10, 6, 3, 8, 9
In-order: 7, 4, 2, 10, 5, 6, 1, 8, 3, 9
Post-order: 7, 10, 6, 4, 5, 8, 9, 2, 3, 1
Pre-order: 1, 2, 4, 7, 5, 10, 6, 3, 8, 9
In-order: 7, 4, 2, 10, 5, 6, 1, 8, 3, 9
Post-order: 7, 4, 10, 6, 5, 2, 8, 9, 3, 1
Pre-order: 1, 2, 4, 7, 5, 10, 6, 3, 8, 9
In-order: 7, 4, 2, 10, 5, 6, 1, 8, 3, 9
Post-order: 7, 4, 10, 6, 5, 2, 8, 9, 3, 1

Answer: (d) Pre-order: 1, 2, 4, 7, 5, 10, 6, 3, 8, 9

In-order: 7, 4, 2, 10, 5, 6, 1, 8, 3, 9

Post-order: 7, 4, 10, 6, 5, 2, 8, 9, 3, 1

Explanation:

In pre-order traversal, we first traverse the root node followed by its left predecessors, then the right predecessors.

So, the correct pre-order sequence would be 1, 2, 4, 7, 5, 10, 6, 3, 8, 9.

In in-order traversal, we first traverse the left predecessors, followed by the right predecessors and then the root node.

So, the correct in-order sequence would be 7, 4, 2, 10, 5, 6, 1, 8, 3, 9.

In post-order traversal, we first traverse the left predecessors, followed by the right predecessors and then the root node.

So, the correct post-order sequence would be 7, 4, 10, 6, 5, 2, 8, 9, 3, 1

Therefore, (d) is the correct answer.

18) Which of the listed pairs of traversals is insufficient to create a unique binary tree?

Pre-order and In-order
Pre-order and Post-order
Post-order and In-order
None of the above

Answer: (b) Pre-order and Post-order

Explanation:

Pre-order and post-order sequences are not insufficient to create a unique binary tree.

Let's take an example, the pre-order and post-order traversal of a binary tree are 123 and 321, respectively.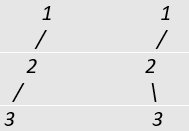

Here, both the trees have the same pre-order and post-order sequences. We can't say which one is the actual one. Pre-order and post-order sequences do not provide enough details about a node's single child to distinguish whether it is a left or a right child.

To uniquely create a binary tree, the in-order sequence is compulsory.

Therefore, (b) is the correct answer.

19) An empty binary search tree is filled with the following integers in the specified order: 10, 1, 3, 5, 15, 12, and 16. How tall is the binary search tree (the height is the farthest leaf node can be from the root, which means the root is at level 0)?

Answer: (b) 3

Explanation:

The following are the characteristics of the binary search tree:

Only nodes with keys smaller than the node's key are present in the left subtree of a node.
Only nodes with keys larger than the node's key are found in the right subtree of a node.
A binary search tree must also be present in the left and right subtrees.

After inserting the given integers in the provided sequence, we get the following Binary Search Tree: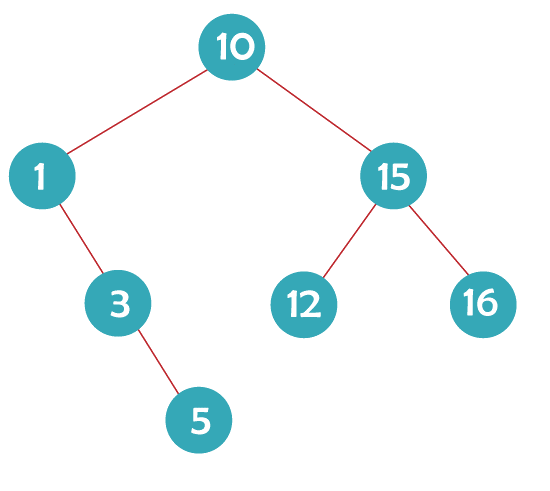

The height of the binary tree is 3. Hence, (b) is the correct answer.

20) What benefit does the adjacency list representation of a graph provide over the adjacency matrix format, specifically?

Space is conserved for sparse graphs in adjacency list form.
DFS and BSF for adjacency list representation can be completed in O(V + E) time. In the representation of an adjacency matrix form, these operations take O(V2) time. Here, V and E are the respective numbers of vertices and edges.
It is simpler to add a vertex to an adjacency list representation than an adjacency matrix form.
All of the above

Answer: (d) All of the above.

Explanation:

Adjacency Matrix: A graph is represented as a two-dimensional array in the adjacency matrix representation. The array has a size of V x V, where V is the collection of vertices.

Adjacency List: A graph is represented as an array of linked lists in the adjacency list format. An edge between two vertices is represented by each element in the linked list that the array's index represents.

The adjacency list provides all the mentioned benefits over the adjacency matrix.

Therefore, (d) is the correct answer.

Next TopicComputer Science Quiz - III: Part 2

← prev next →