Computer Science Quiz - III: Part 2Topic - 6 Algorithms1) Assume that T(n) is a function that the recurrence defines. T(n) = 2T(n/2) + n when n >= 2 and T(1) = 1, Which of the following claims is accurate?
Answer: (a) T(n) = O(n) Explanation: Given Recurrence Relation: T(n) = 2T(n/2) + n ... (i) Using Masters' Theorem: T(n) = aT(n/b) + f(n) ... (ii) Comparing (i) and (ii), we get a = 2, b = 2, and f(n) = n Case I: f(n) = O(n^logba) n = O(n^log22) n = O(n^1) n = O(n), Equation holds Hence, T(n) = O(n). Therefore, (a) is the correct answer. 2) There is a total of25 horses, and you need to identify the top 3 speed horses. To determine their relative speeds, races can be held between a maximum of five horses. You can never determine the horse's true speed in a race. Identify the number of races necessary to findthe top three horses.
Answer: (c) 7 Explanation: Run 5 races with the horses divided into 5 groups. Take the winners of the first five races and run thesixth race; the winner of this race will be the fastest of 25horsesoverall. Run the seventh race now with the following horses. 1) The second and third-place horses in the sixth race 2) Select the second and third-fastest horses in the group that are tied for first in the sixth race. 3) Select the animal in the group that finished second fastest in the sixth race. The fastestand secondfastest of the7th raceare the secondfastest and third fastestof all 25 horses, respectively. Therefore, (c) is the correct answer. 3) There are n unique elements in an unordered list. To discover an element in this list that is neither the maximum nor the minimum, comparisons must be made a total of
Answer: (d) O(1) Explanation: We simply need to compare any 3 of the elements. The middle element of the three will be one of the not maximum and minimum elements. Since there are constant numbers of comparisons, the time complexity is (1). Therefore, (d) is the correct answer. 4) Two lists are supposed to be concatenated in O(1) time. Which of the subsequent list implementations should be used?
Answer: (d) Circular Doubly Linked List Explanation: Singly, doubly, and circular singly linked lists cannot be used to implement the given idea as we do not have a pointer to the last node. To concatenate two lists of either type, we need to traverse one of the lists to get access to the last node, which requires O(n) time. A circular doubly linked list can be concatenated in constant time O(1). We only need to execute the correct sequence of code. Let the front and last of the pointer of list1 and list2 be front1 and last1 and front2 and last2, respectively. last1 -> next = front2 front2 -> prev = last1 front1 -> prev = last2 last2 -> next = front We can rename the pointer of the new node as front = front1 and last = last2. 5) The worst-case time complexities of the Tower of Hanoi with n disks problem, the binary search on the sorted list of n elements, the quick sort on an array of n elements and the heap sort on an array of n elements are as follows
Answer: (d) O(2n), O(logn), O(n2), O(n logn) Explanation: The Tower of Hanoi is a mathematical puzzle in which we are given n disks of different sizes and three rods starting, ending and auxiliary. The objective of the puzzle is to move all the disks from the starting rod to the ending rod, and the rules are:
The time complexity of this problem is O(2n). In the worst-case, the time complexity of binary search is O(logn) In the worst-case, the time complexity of heap sort remains O(n logn) but the time complexity of quick sort changes to O(n2). 6) 6 Q Take into account the following claims: I. A leaf node is always where a max-smallest heapelement can be found. II. The root node's child is always the second-largest element in a max-heap. III. A binary search tree can be used to quickly create a max-heap in Q(n) time. IV. A max-heap can be converted into a binary search tree in Q(n) time. Which of the aforementioned claims is true?
Answer: (b) I, II, and III Explanation: The first statement is true. Leaf nodesin a max heap always containthe smallest element. Therefore, we must search for the minimum value for each leaf node. The worst-case complexity is O(n). The second statement is also true. The largest element is always found at the top, and the second largest element is always the root child. The third statement is true because building a max heap requires O(n) time. The fourth statement is false since it takes O(n logn) time to create a binary search tree from a max-heap. Therefore, (b) is the correct answer. 7) When used on an array that is sorted or nearly sorted, which of the following sorting algorithms, in its typical implementation, performs the best (maximum 1 or two elements are misplaced)?
Answer: (d) Insertion Sort Explanation: In the best case, the time complexity of insertion sort becomes O(n) since it compares the elements and inserts them at their right position. So, when it comes to sorting a nearly sorted array, it will not take more time. On the other hand, heap sort, and merge sort will take O(n logn) time, and quick sort will take O(n2) will be the worst. 8) Think about a scenario where a swap procedure is exceedingly expensive. Which of the following sorting algorithms ought to be chosen in order to reduce the overall number of swap operations?
Answer: (b) Selection Sort Explanation: The selection sort selects the minimum or the maximum and swaps the element with its correct position. It does not take more than O(n) swaps. Selection sort performs best when it comes to number of swaps required. 9) If an element in an array X is larger than every element to its right, it is referred to as the leader of the array. a good approach for finding every leader in an array
Answer: (b) Use a right-to-left pass of the array to solve it in linear time Explanation: The plan is to count up the most elements that have been reached so far while scanning the array's elements from right to left. Print the value whenever the maximum fluctuates. To put the concept into practice, take the following actions:
This can be done in linear time. Hence, (b) is the correct answer. 10) Assume that G is an undirected weighted graph and e is an edge in G with the maximum weight. Consider the minimum weight spanning tree in G that has the edge e in it. That which is always TRUE among the following statements?
Answer: (b) All the edges in a cut set in G are of maximum weight Explanation: Consider the following graph taken as an example: 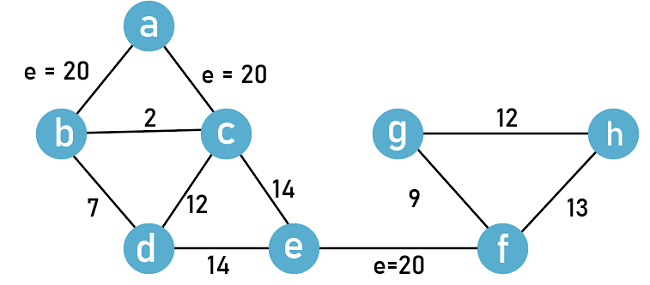
There are three edges with maximum weight. The edge ef will be the part of the mst. A cut set is defined as the set of edges by removing them disconnects the graphs. Option A: This statement is false because we cannot conclude that each edge is of unique weight. Although edges can be the same weight. Option B: The cut set {ab, ac} contains both the edges of maximum weight. Hence, option (b) is true. Option C: This statement is false. Here, we have the option to choose between edges ab and ac. So, we can guarantee uniqueness. Option D: This statement is also false. There are possibilities that e can be a part of a cycle. 11) The appropriate data structure usedto utilize in order to implement Dijkstra's shortest path algorithm on unweighted graphs is:
Answer: (b) Heap Explanation: Both the heap and the priority queue are particularly attractive data structuresallowing:
Maintaining a list of components and searching through it for the one with the highest priority is a straightforward approach to create a heap or priority queue data type. This gives Dijkstra's shortest path algorithm on an unweighted graph an implementation time of O(n). 12) Which of the following claims about the Bellman-Ford shortest path algorithm is true? I. If there is a negative weighted cycle, it is always found. II. Determines whether any negative weighted cycle can be reached from the source.
Answer: (b) Only II Explanation: The Bellman-Ford shortest path algorithm is used to determine a single-sourceshortest path. Therefore, it can only detect cycles that can be reached from a certain source and cannot find cycles with anegative weight that are not reachable from the given source. Think about a disconnected situation where a negative weight cycle cannot be reached at all from the source.If there is a negative weight cycle reachable from the source, after (number of vertices- 1)number of iterations, the algorithm will detect it. So, saying it will always find the negative weight cycle is wrong. Hence, the statement I is false, and the statement II is true. 13) Think about the tree arcs of a BFS traversal starting at source node W in an unweighted, connected, undirected graph. Using the tree T created by the tree arcs, one may compute
Answer: (b) The shortest route from W to each graph vertex Explanation: The tree formed by doing BFS traversal from node W gives shortest path of all the nodes from W. In an unweighted graph, BFS always finds the shortest route from the source to every other vertex. Therefore, (b) is the correct answer. 14) Assume that G is an undirected connected weighted graph with a set of distinct positive edge weights. Which of the following statements (if any) is/are TRUE if each edge weight is increased by the same amount? I. There will be no change in the minimum spanning tree. II. The shortest distance between all the vertices will remain same.
Answer: (a) Only I Explanation: The shortest route might alter. The reason is thatany pair of edges, such as a and b, may have a different number of edges in various pathways. For illustration, suppose the shortest path between a and bhas 4edges and a weight of 12. Allow for a second path with two edges and a weight of 17. The weight of the shortestpath after incrementing each edge weight with 5is now 12+ 4*5 = 32. The other path's weight is boosted by 2*5, making it 17+ 10 = 27. Thus, the shortest way switches to another path with aweight of 27. There is no modification to the Minimum Spanning Tree. Keep in mind that in Kruskal'salgorithm, the edges are sorted first. If all weights are increased, the edges' order won't change. 15) What is the weight of the minimum spanning tree of the given graph? 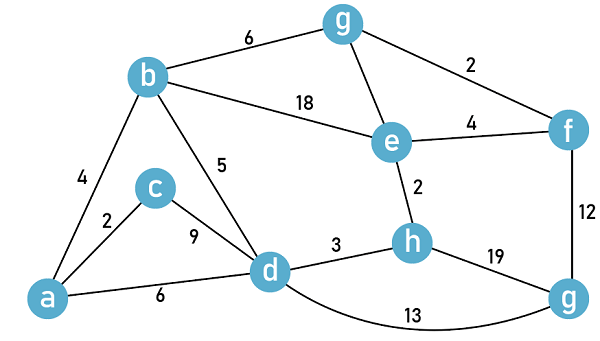
Answer: (c) 34 Explanation: Using Kruskal's algorithm, we first sort all the edges in descending edge weight. And try to select the edges with minimum edge weight and we have to make sure we avoid any type of cycle formation in the spanning tree:
So, the weight of the minimum spanning tree = 2 + 2 + 2 + 3 + 4 + 4 + 5 + 12 = 34. Therefore, (c) is the correct answer. 16) The Floyd Warshall algorithm for computing all-pair shortest routes is based on the following:
Answer: (b) Dynamic Programming Explanation: All pairs of shortest-path issues can be resolved using the Floyd Warshall algorithm. Finding the shortest distances between each pair of vertices in an edge-weighted directed graph is the goal of the problem. Dynamic programming serves as its foundation. Therefore, (b) is the correct answer. 17) Consider a chain of matrices that have been multiplied: A1 x A2 x A3 x A4 x A5, where A1, A2, A3, A4 and A5 matrices with dimensions of 5 x 10, 10 x 35, 35 x 15, 15 x 25, and 25 x 100 respectively. What will the minimum total number of scalar multiplications in the parenthesisation of A1 x A2 x A3 x A4 x A5 be _____________?
Answer: (a) 18775 Explanation: Formula to calculate the cost of multiplication: m[i, j] represents the cost of multiplying matrix number i to j. m[i, j] = { 0 if (i == j)} m[i, j] = { min[m[i, k] + m[k+1, j] + Pi-1 Pk Pj] if (i < j)} The range of k will be i <= k < j. We will calculate the cost on each value of k and select the minimum cost. We have created this table using the matrix dimension:
The cost of multiplying one matrix is zero that's why we have filled zero in the respective cells. Now, calculating m[1, 2]. The possible value of k is 1. For k = 1: m[1, 2] = m[1, 1] + m[2, 2] + P0* P1* P2 = 0 + 0 + 5 * 10 * 35 = 1750 Similarly, we can find the cost of m[2, 3], m[3, 4] and m[4, 5]. Now, calculating m[1, 3]. The possible values of k = 1, 2 For k = 1: m[1, 3] = m[1, 1] + m[2, 3] + P0 * P1 * P3 = 0 + 5250 + 5 * 10 * 15 = 0 + 5250 + 750 = 6000 For k = 2: m[1, 3] = m[1, 2] + m[3, 3] + P0 * P2 * P3 = 1750 + 0 + 5 * 35 * 15 = 4375 We have got the minimum cost for k = 2. Similarly, we can calculate the cost of m[2, 4] and m[3, 4]. The complete table will look like the following: 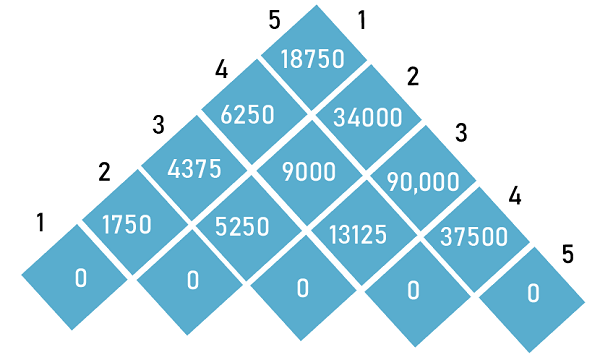
The cost of multiplying the matrices is 18750. 18) In order to find the longest common subsequence between two strings,we use the concept of dynamic programming. Using an array L[M, N], the values of L(i, j) could be determined using dynamic programming based on the correct recursive definition of L(i, j). Which of the following claims about the dynamic programming answer to the recursive definition of L(i, j) is TRUE?
Answer: (b) Both a row-majororder and a column-majororder of L(M, N)can be used to compute the values of l(i, j). Explanation: Option A is False because it is not necessary to initialized all the elements of L[M, N] to 0. We only fill zeros in the first row and the first column. Option B is True. By doing the computation either in row major or column major, we can perform the desired computation. Option C is False. It negates the option B which is not true. Option D is False because to compute the value of l[i, j], we only need the values of l[i-1, j], l[i, j-1] and l[i-1, j-1]. The condition p<r or q<s do not completely satisfy the condition. 19) Match the following:
Answer: (c) A - (iii), B - (iv), C - (i), D - (ii) Explanation:
Therefore, option (c) is the correct answer. 20) Think about the sequence abbbcddddee. Each letter in the string needs to have a binary code that meets the requirements listed below:
What is the shortest encoded string length among all the binary code assignments that meet the two properties mentioned above?
Answer: (a) 24 Explanation: The properties mentioned in the question are the same as for Huffman coding. We will follow two basic rules here: i. For creating a Tree, we will select the alphabet with the minimum frequency and create the Huffman tree in bottom-up fashion. ii. We will assign binary 1 to the right edge of a node and binary 0 to the left edge of a node. To assign the code, we will traverse the tree from the root to all the leaf nodes containing alphabet.
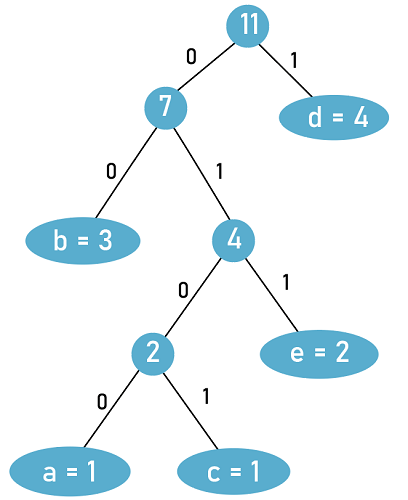
Binary Code Assigned to each alphabet: a - 0100, Length = 4 b - 00 , Length = 2 c - 0101, Length = 4 d - 1, Length = 1 e - 011, Length = 3 Shortest length of the string in binary = 4 * 1 + 2 * 3 + 4 * 1 + 1 * 4 + 3 * 2 = 4 + 6 + 4 + 4 + 6 = 24 Therefore, (a) is the correct answer.
Next TopicComputer Science Quiz - II: Part 1
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









