Linear Programming in Excel
This tutorial demonstrates how to use Excel to tackle integer linear programming problems. With the Solver add-in in Microsoft Excel, users may find the solution for an integer linear program rapidly. We will walk through this process in simple, straightforward steps today. The final portion of this tutorial will also see an example of a mixed-integer linear programming problem. So, let's begin without delay.
Integer Linear Programming
Integer linear programming uses integer variables, linear objective functions, and equations. The minimal or maximum result of a particular problem under certain conditions can be found using linear programming. It is an instrument that can be utilized to find the most effective strategy to use the scarce resources. There are several key components to all forms of linear programming. Below are their details:
- Decision Variables: We ascertain which choices will reduce or maximize the goal function.
- Objective Function: The objective function aids our ability to identify the decision variables. It conveys how the variables and the outcome are related.
- Constraints: Constraints are additional functions that indicate various requirements for potential resolutions.
In addition to integer linear programming, a mixed-integer linear programming example will be shown. There are continuous and integer variables in mixed-integer linear programming.
Excel Step-by-Step Instructions for Solving Integer Linear Programming
We'll use an example to demonstrate step-by-step methods. To understand the essential concepts, you must attentively read them. You must carefully read the question and determine the Objective function and Constraints.
Let's say that two goods that can be swapped out are produced by a machine. The machine can produce ten units of item 2 and a maximum of twenty units of item 1 each day. Another option is to set the machine to create a maximum of 22 units of item 1 and 18 units of item 2 daily. According to market analysis, the overall daily demand for the two goods is 40 units. When choosing between the two machine settings, which should be chosen given that the unit earnings for the two items are $15 and $18?
Step 1: Examine the Question and Establish a Dataset
- Before anything else, we must fully comprehend and thoroughly examine the provided integer linear programming problem.
- The results of the analysis of the query above are shown below.
Decision Variables:
- X1: The product's production amount
- X2: The amount of product produced 2.
- Y: 1 in the case of the first setting picked, 0 in the case of the second setting selected.
Objective Function:
In this case, the objective function is:
Constraints:
The question above primarily leads us to three limits. These are:
According to the market analysis, 40 combined units of the two items are the maximum daily demand.
For product 1, only this constraint applies.
For the second product, it serves as a limitation.
Y will either be zero or one.
There cannot be a negative quantity of products.
- Considering the constraints, functions, and variables, we generated a dataset in the subsequent step that looks like the image below. You are free to modify it to suit your needs.
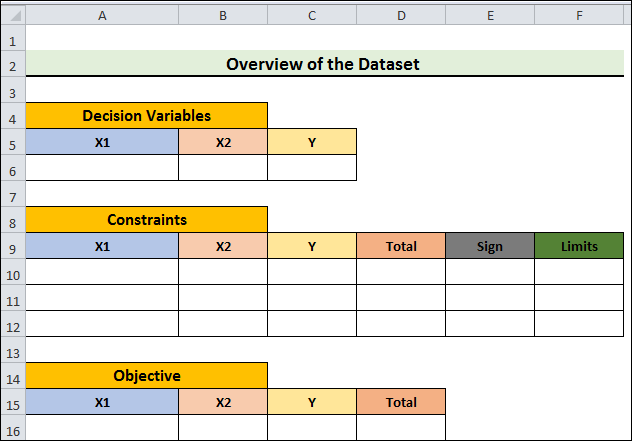
Step 2: Open Excel and load the solver add-in
- Second, we must open Excel and load the Solver add-in. You can proceed to step 3 when the data has already been in Excel.
- Click the File tab to accomplish this.
- Next, choose Options by clicking on it in the left-bottom corner of the screen.
- Excel Options will open as a result.
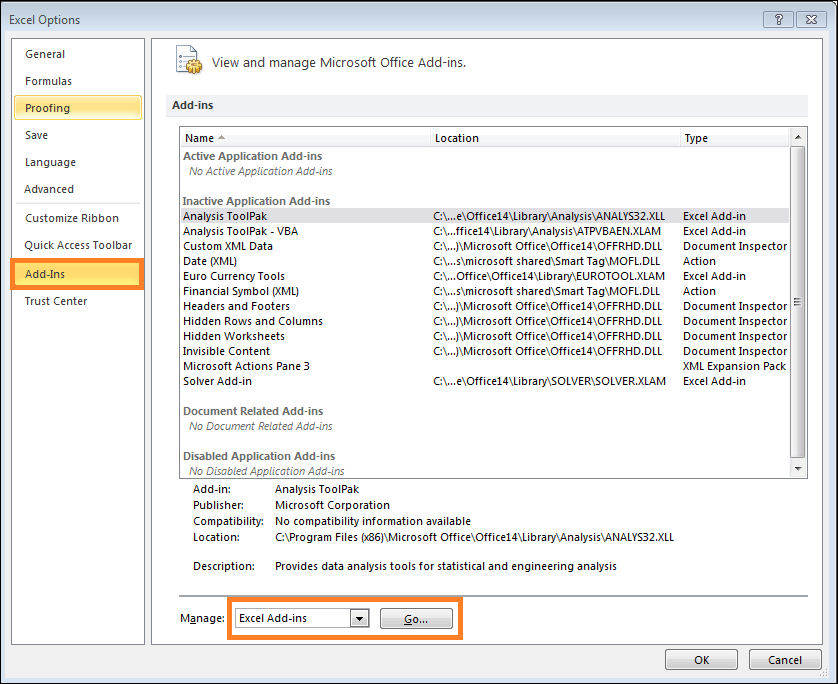
- Select Add-ins from the Excel Options windows.
- Next, in the Manage box, choose Excel Add-ins, then click Go.
- There will be a message box about add-ins displayed.
- Choose OK from the notification box after checking the Solver Add-in.
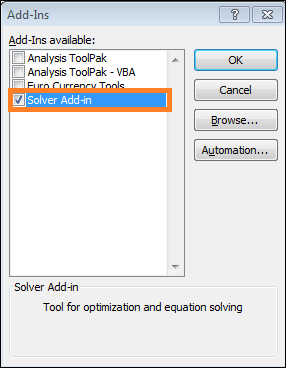
- Finally, you can see the Solver feature under the Analysis section of the Data tab.

Step 3: Fill in the Objective Function and Constraints Coefficients
- Thirdly, the dataset's objective function and constraints must be filled in.
- This is where we will mostly insert the objective function and constraint coefficients.
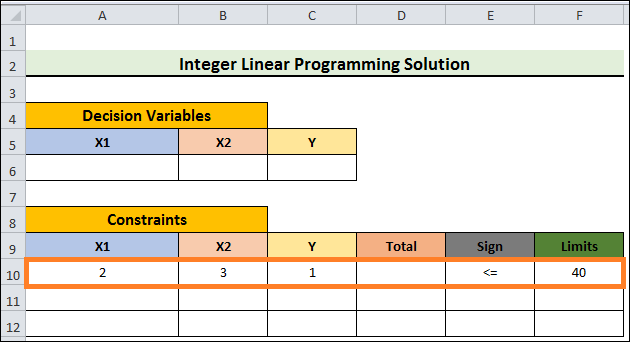
- 2X1+3X2<=40 is our initial constraint. This indicates that the products' total should equal 40 or fewer if the initial setting is used.
- For X1 and X2, respectively, the coefficients are 2 and 3.
- Furthermore, the coefficient of Y is 1 because the equation shows the initial configuration.
- It has a <= sign.
- Furthermore, 40 is the upper limit.
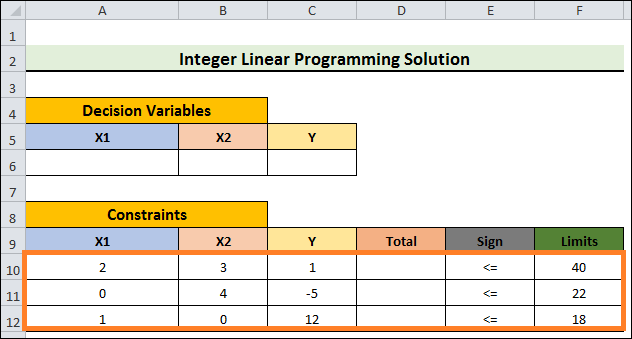
- Follow the previous instructions again, entering the coefficients for each constraint.
- Next, choose Cell D10 and enter the following formula:
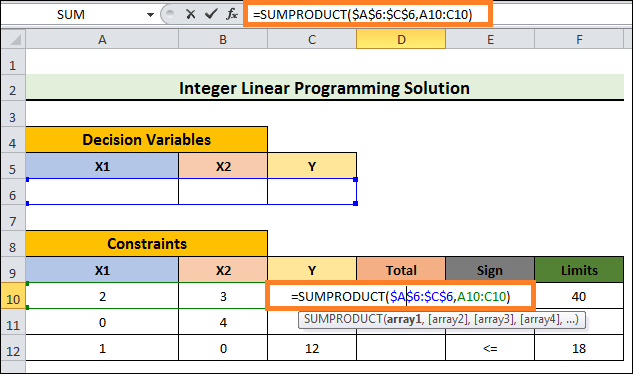
The SUMPRODUCT function was utilized in this formula to compute the product of the decision variables and the relevant constraints variables, which were then added. Cell A6 will multiply by Cell A10, Cell B6 by Cell B10, & Cell C6 by Cell C10. Subsequently, every product will be combined.
- Press Enter and drag the Fill Handle.
- Now, complete Cells A16 through B16 with the objective function's coefficients.
- Z = 6X1+8X2 is the objective function in our scenario.
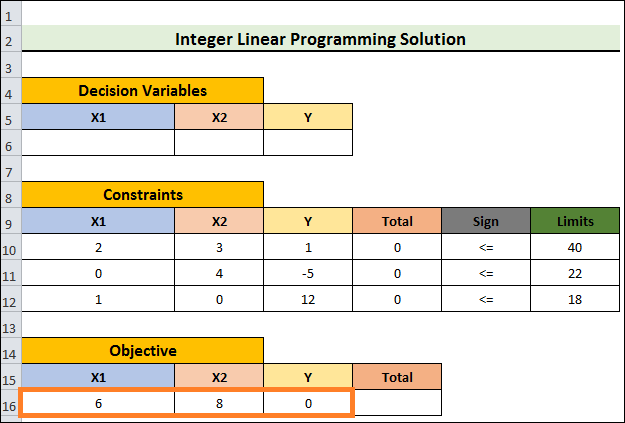
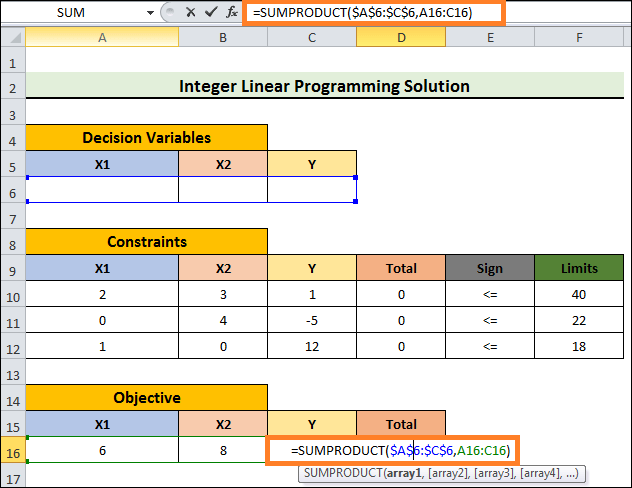
- Choose Cell D16 once more, then enter the following formula:
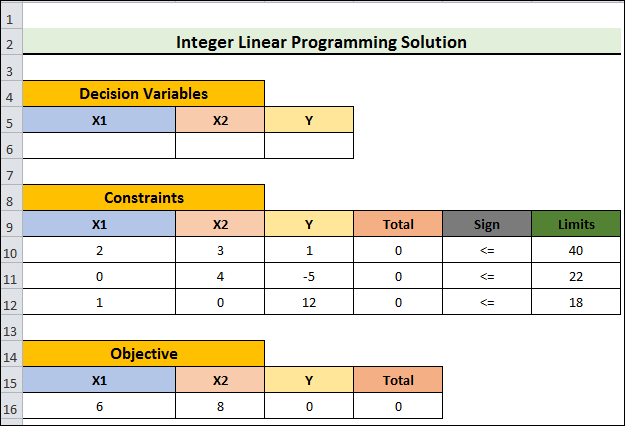
- After inputting the coefficients and formulas, hit Enter to view a dataset like the one below.
Step 4: Enter the parameters for the Solver
- Step 4 involves selecting Solver from the AnalysIis section under the Data The window for the solver parameters will open.

- You must enter the Cell holding the objective function's value within the Set Objective box.
- Thus, we have $D$16 typed here.
- In this case, maximizing the outcome is our goal.
- On the type $A$6:$C$6 in the "By Changing Variable Cells," the variables for making decisions are included.
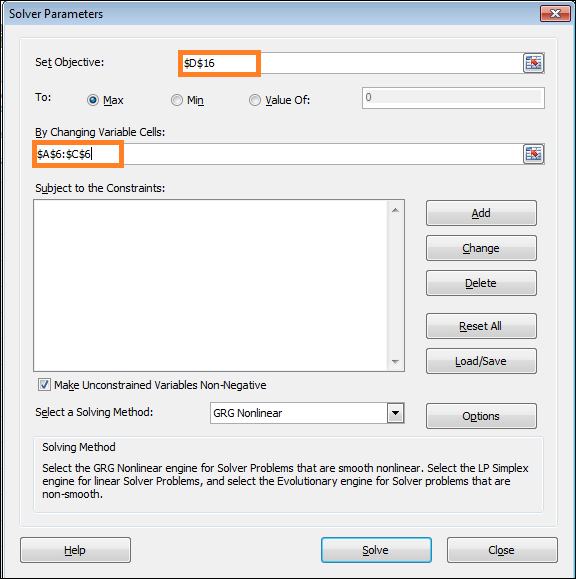
Step 5: Add in Subject to Constraints
- Subjects must be added to the constraints in the fifth stage.
- The relationship between the restrictions and the variable type-binary or integer-must be indicated.
- Please select Add for that reason. The Add Constraint dialogue box will be shown.
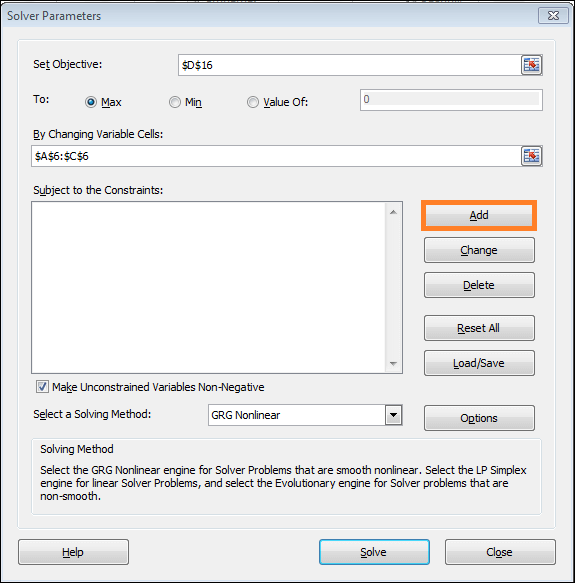
- Select the bin using the drop-down option after typing $C$6 within the Cell Reference box of the Add Constraint dialogue.
- Y is either 0 or 1. Cell C6 contains this value. It suggests binary numbers. We chose this particular bin for this reason.
- Click OK to continue.
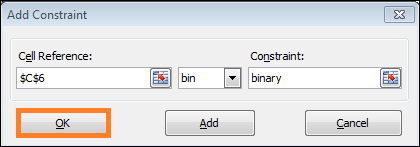
- Once more, select Add.
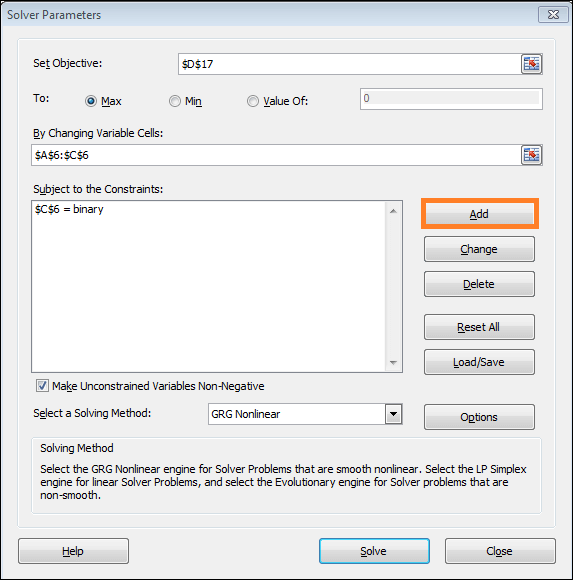
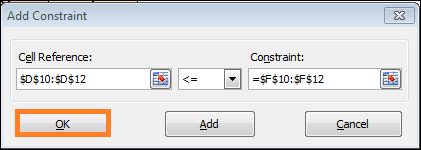
- This time, fill out the Cell Reference box with $D$10:$D$12, select the <= symbol through the drop-down menu, & enter =$F$10:$F$12 in its Constraint box.
- Next, press OK.
- From the Solver Parameters window, click Add once more.
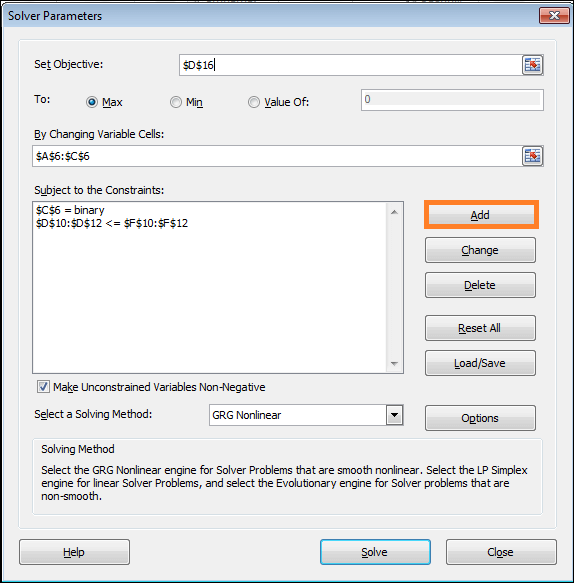
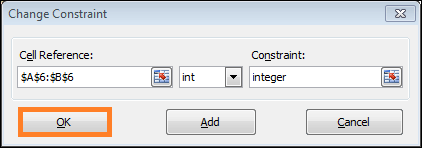
- Enter $A$6:$B$6 into the Cell Reference field now, and choose it in the drop-down list.
- The values of integers X1 and X2 are stored in cells A6 and B6.
- Once more, press OK.
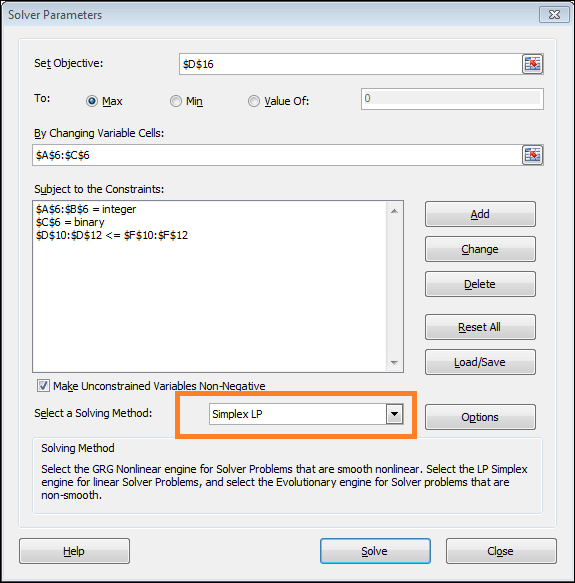
Step 6: Choose the Method for Solving
- When prompted to "Select a Solving Method," in step 6, choose Simplex LP and press Solve.
- A check for "Make Unconstrained Variables Non-Negative" should be made.
- The Solver Outcomes window will open after selecting Solve.
- After that, choose OK.
Step 7: The Integer Linear Programming Solution
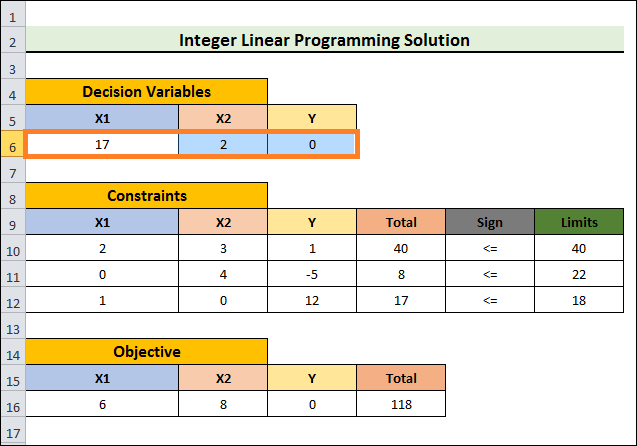
- In the Excel sheet, you will ultimately locate the solutions in the cells you want.
- We will get the greatest results in this instance using the second machine option.
Step 8: Create an Answer Report
- You can also generate the response report.
- Choose Answer from the Reports area of the Solver Results box and click OK to accomplish that.
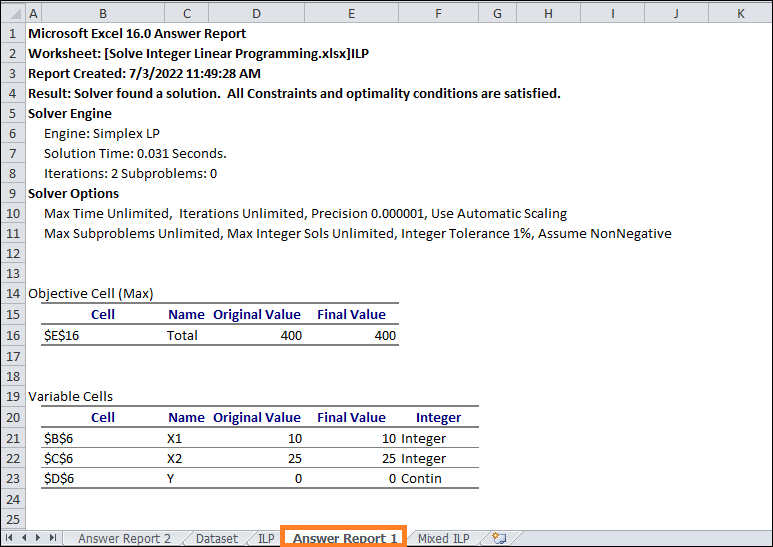
- The report is finally located on another sheet.
Example of Mixed Integer Linear Programming in Excel
This part will discuss a straightforward Excel mixed-integer linear programming example. The easy steps for solving mixed-integer linear programming using Excel are as follows. Let us examine the objective function & its corresponding constraints in this scenario.
The Objective Function:
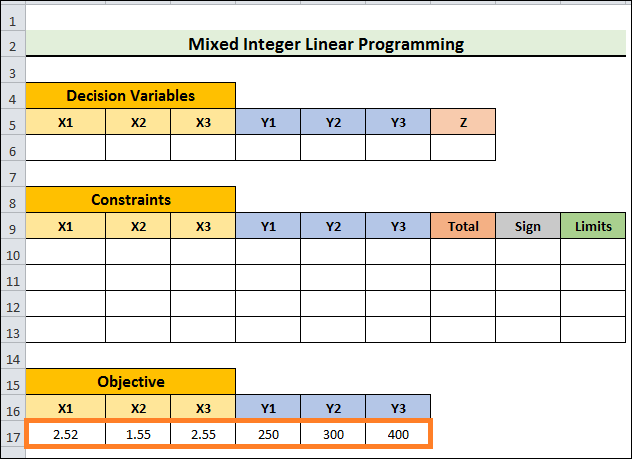
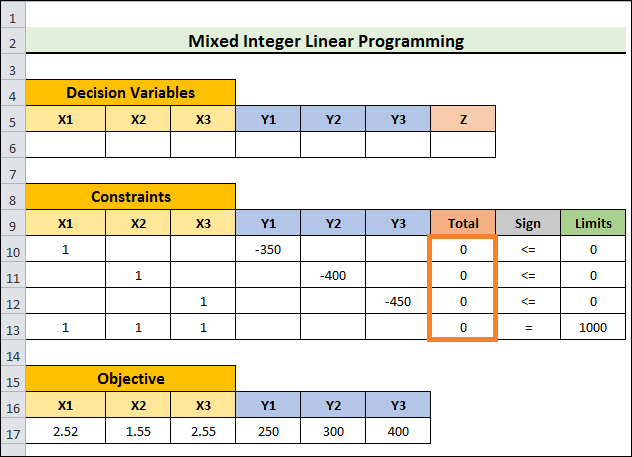
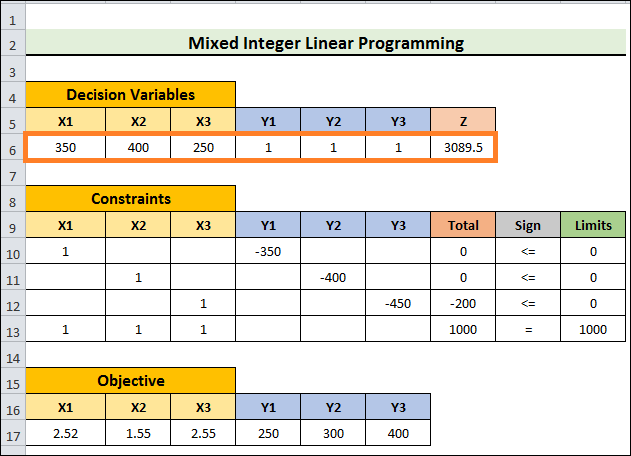
- Z = 2.52X1+1.55X2+2.55X3 + 250Y1 + 300Y2 + 400Y3
Constraints:
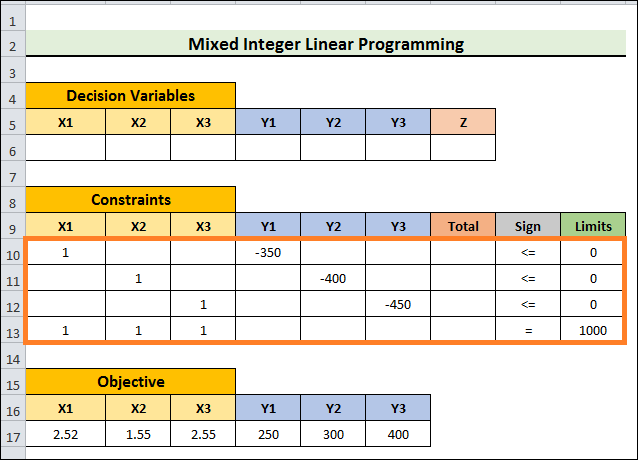
- X1-350Y1<=0
- X2-400Y2< = 0
- X3-450Y3<=0
- X1+X2+X3=1000
In this instance, the variables X1, X2, and X3 were integers. However, Y1, Y2, & Y3 are binary numbers. We also need to determine Z's lowest value.
Let's take the steps listed below to understand everything there is to know about the example.
STEPS:
- Construct a dataset to hold the Decision Variable, Constraint, and Objective Function coefficients.
- Second, look up the mixed coefficients for the Objective Function's variables.
- Thirdly, enter the coefficients for the Constraint variables, as shown in the image below. Let the Total column remain blank.
- Next, choose Cell G10 and input the following formula:
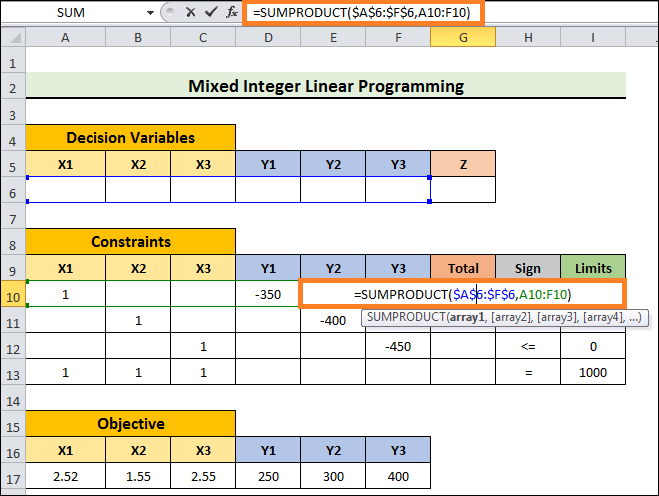
- To drop the fill handle, press Enter.
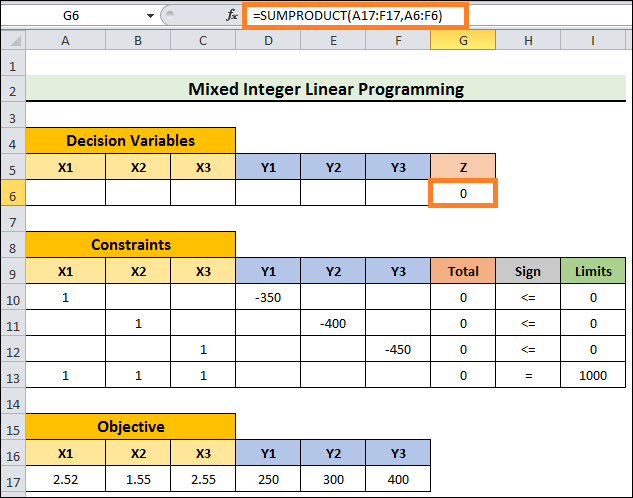
- Enter the following formula in cell G6 now:
- Press Enter.
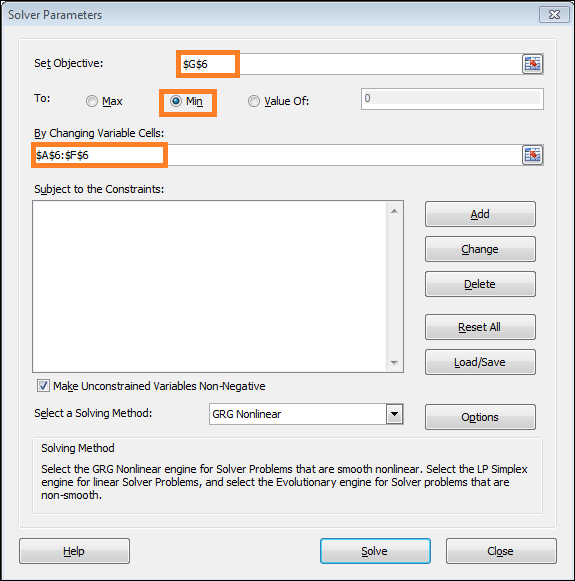
- Go to the Data tab and choose Solver in the next step. The window for Solver Parameters will open as a result.

- Make the objective in Cell $G$6 to Min within the Solver Parameters window by adjusting the variable cells $A$6:$F$6.
- Click Add after that.
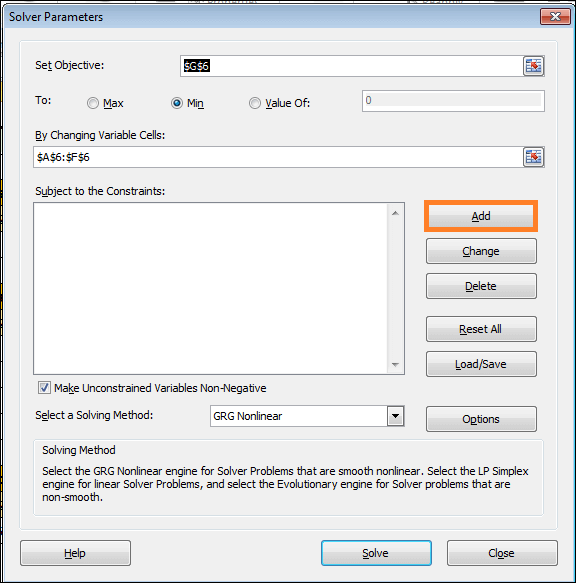
- Add constraints one at a time, and select Simplex LP for the solution method.
- For further action, click Solve.
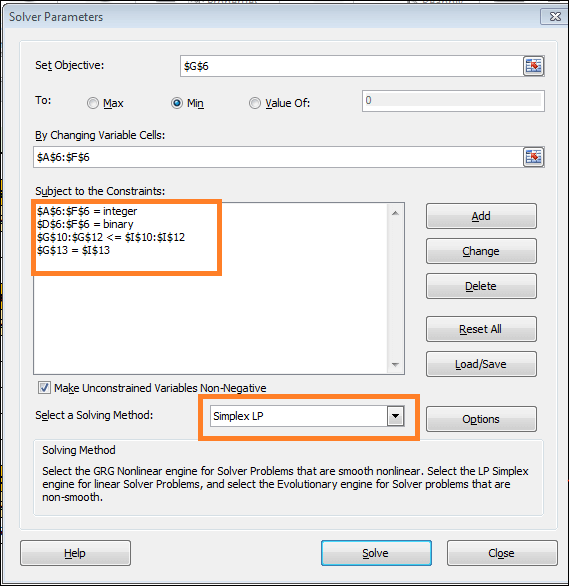
- It will then bring up the Solver Results window.
- Next, click OK.
- The outcome will eventually resemble the image below.
|




 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now











































